
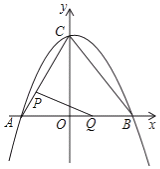
【题目】如图,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)求二次函数的解析式;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)在点P,Q运动过程中,△APQ不可能是直角三角形,理由详见解析;(3)M(1,4)或(
x+4;(2)在点P,Q运动过程中,△APQ不可能是直角三角形,理由详见解析;(3)M(1,4)或(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4).
,﹣4).
【解析】
(1)判断出抛物线的解析式中二次项系数,再利用交点式,即可得出结论;
(2)分两种情况:当∠AQP=90°,判断出点P在y轴右侧,不符合题意,当∠APQ=90°时,根据相似三角形的性质得出比例式,建立方程求出t的值,而t大于4,也不符合题意,即可得出结论;
(3)先求出△AOC的面积,进而得出△AOM的面积,进而建立方程求解即可得出结论.
解:(1)∵二次函数y=﹣![]() x2+bx+c过点A(﹣3,0),B(4,0),
x2+bx+c过点A(﹣3,0),B(4,0),
∴抛物线的解析式为y=﹣![]() (x+3)(x﹣4)=﹣
(x+3)(x﹣4)=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)在点P,Q运动过程中,△APQ不可能是直角三角形,
理由:由(1)知,抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4,
x+4,
∴C(0,4),
∵A(﹣3,0),B(4,0),
∴AC=5,OA=3,OC=4,
由运动知,AP=t,OQ=t,
∴AQ=3+t,(0<t<4)
∵∠OAP是Rt△AOC的一个锐角,
∵△APQ是直角三角形,
①当∠AQP=90°时,
∵∠AOC=90°=∠AQP,
∴PQ∥y轴,
∵点Q在OB上,
∴点P不可能在第二象限内,此种情况不存在,
②当∠APQ=90°时,
∵∠AOC=90°=∠APQ,
∵∠PAQ=∠OAC,
∴△AOC∽△APQ,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
∵0<t<4,
∴此种情况不符合题意,
即在点P,Q运动过程中,△APQ不可能是直角三角形;
(3)由(2)知,OA=3,OC=4,
∴S△AOC=![]() OAOC=6,
OAOC=6,
∵△AOM的面积与△AOC的面积相等,
∴S△AOM=6,
设点M(m,﹣![]() m2+
m2+![]() m+4),
m+4),
∴S△AOM=![]() OA|﹣
OA|﹣![]() m2+
m2+![]() m+4|=
m+4|=![]() |﹣
|﹣![]() m2+
m2+![]() m+4|=6,
m+4|=6,
∴m=0(舍)或m=1或![]() ,
,
∴M(1,4)或(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4).
,﹣4).


科目:初中数学 来源: 题型:
【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:6cos45°+(![]() ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3![]() |+42017×(﹣0.25)2017;
|+42017×(﹣0.25)2017;
(2)先化简,再求值:(![]() ﹣a+1)÷
﹣a+1)÷![]() ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
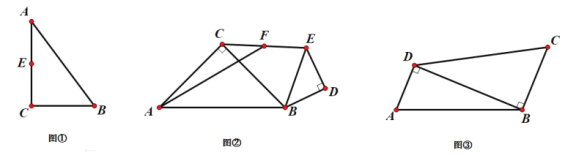
(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,将
边上,将![]() 沿着
沿着![]() 折叠后得到
折叠后得到![]() ,连接
,连接![]() 并使得
并使得![]() 最小,请画出符合题意的点
最小,请画出符合题意的点![]() ;
;
问题探究:
(2)如图②,已知在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,求
,求![]() 的最大值;
的最大值;
问题解决:
(3)西安大明宫遗址公园是世界文化遗产,全国重点文物保护单位,为了丰富同学们的课外学习生活,培养同学们的探究实践能力,周末光明中学的张老师在家委会的协助下,带领全班同学去大明宫开展研学活动.在公园开设的一处沙地考古模拟场地上,同学们参加了一次模拟考古游戏.张老师为同学们现场设计了一个四边形![]() 的活动区域,如图③所示,其中
的活动区域,如图③所示,其中![]() 为一条工作人员通道,同学们的入口设在点
为一条工作人员通道,同学们的入口设在点![]() 处,
处,![]() ,
,![]() ,
,![]() ,
,![]() 米.在上述条件下,小明想把宝物藏在距入口
米.在上述条件下,小明想把宝物藏在距入口![]() 尽可能远的
尽可能远的![]() 处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出
处让小鹏去找,请问小明的想法是否可以实现?如果可以,请求出![]() 的最大值及此时
的最大值及此时![]() 区域的面积,如果不能,请说明理由.
区域的面积,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,点O在BC上,以线段OC的长为半径的⊙O与AB相切于点D,分别交BC、AC于点E、F,连接ED并延长,交CA的延长线于点G.
(1)求证:∠DOC=2∠G.
(2)已知⊙O的半径为3.
①若BE=2,则DA= .
②当BE= 时,四边形DOCF为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AB=AC,∠A=40O,延长AC到D,使CD=BC,点P是ΔABD的内心,则∠BPC=

A. 105° B. 110° C. 130° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com