
【题目】(1)计算:6cos45°+(![]() ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3![]() |+42017×(﹣0.25)2017;
|+42017×(﹣0.25)2017;
(2)先化简,再求值:(![]() ﹣a+1)÷
﹣a+1)÷![]() ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
【答案】(1)5;(2)﹣1﹣a,﹣1.
【解析】
(1)由题意根据特殊角的三角函数值、零指数幂、绝对值、有理数的乘方可以解答本题;
(2)由题意根据分式的加减法和除法可以化简题目中的式子,然后从﹣1,0,2中选一个使得原分式有意义的值代入化简后的式子即可解答本题.
解:(1)6cos45°+(![]() ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3![]() |+42017×(﹣0.25)2017
|+42017×(﹣0.25)2017
=6×![]() +1+5﹣3
+1+5﹣3![]() +[4×(﹣0.25)]2017
+[4×(﹣0.25)]2017
=3![]() +1+5﹣3
+1+5﹣3![]() +(﹣1)2017
+(﹣1)2017
=3![]() +1+5﹣3
+1+5﹣3![]() +(﹣1)
+(﹣1)
=5;
(2)(![]() ﹣a+1)÷
﹣a+1)÷![]() ﹣a
﹣a
=![]() ﹣a
﹣a
=![]() ﹣a
﹣a
=![]() ﹣a
﹣a
=![]() ﹣a
﹣a
=![]() ﹣a
﹣a
=![]() ﹣a
﹣a
=﹣1﹣a,
∵当a=﹣1,2时,原分式无意义,
∴a=0,
当a=0时,原式=﹣1﹣0=﹣1.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
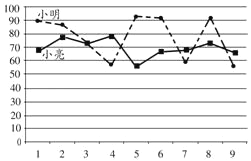
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
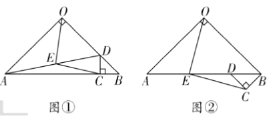
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
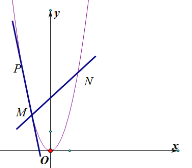
【题目】如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)求抛物线的函数表达式;
(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;
(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在同一平面直角坐标系中有函数y1=ax2﹣2ax+b,y2=﹣ax+b,其中ab≠0.
(1)求证:函数y2的图象经过函数y1的图象的顶点;
(2)设函数y2的图象与x轴的交点为M,若点M关于y轴的对称点M'在函数y1图象上,求a,b满足的关系式;
(3)当﹣1<x<1时,比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
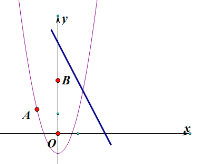
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() 且经过点
且经过点![]() 动直线
动直线![]() 的解析式为
的解析式为![]()
![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 向上平移一个单位得到新的抛物线
向上平移一个单位得到新的抛物线![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点(
两点(![]() 点位于
点位于![]() 点的左边),动直线
点的左边),动直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 的另外一个交点为点
的另外一个交点为点![]() 求证:直线
求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)已知点![]() ,且点
,且点![]() 在动直线
在动直线![]() 上,若
上,若![]() 是以
是以![]() 为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出
为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
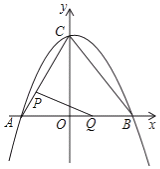
【题目】如图,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)求二次函数的解析式;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)点M在抛物线上,且△AOM的面积与△AOC的面积相等,求出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com