【题目】如图，以40m/s的速度将小球沿与地面30°角的方向击出时，小球的飞行路线是一段抛物线．如果不考虑空气阻力，小球的飞行高度h（单位:m）与飞行时间t（单位:s）之间的函数关系式为h=20t－
(t≥0)． 回答问题:
(1)小球的飞行高度能否达到19.5m；
(2) 小球从最高点到落地需要多少时间?
【答案】（1）19.5m；（2）2s
【解析】
（1）根据抛物线解析式，先求出抛物线的定点，判断小球最高飞行高度，从而判断能否达到19.5m；
（2）根据定点坐标知道，小球飞从地面飞行至最高点需要2s，根据二次函数的对称性，可知从最高落在地面，也需要2s．
（1）h=20t－
由二次函数可知：抛物线开口向下，且顶点坐标为(2，20)，
可知小球的飞行高度为h=20m>19.5m
所以小球的飞行高度能否达到19.5m；
（2）根据抛物线的对称性可知，小球从最高点落到地面需要的时间与小球从地面上到最高点的时间相等．
因为由二次函数的顶点坐标可知当t=2s时小球达到最高点，
所以小球从最高点到落地需要2s．
阅读快车系列答案科目：初中数学 来源： 题型：
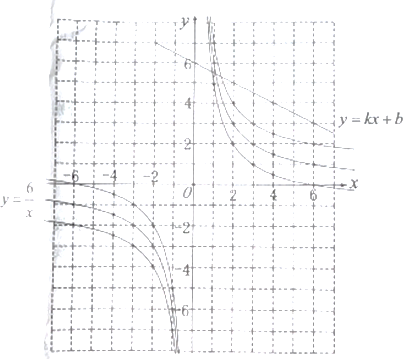
【题目】图象是函数性质的直观载体，通过图象我们容易把握函数的整体性质．下面我们就一类特殊的函数展开探究．经历分析解析式、列表、描点、连线过程得到函数
、
、
的图象如下图所示．
（1）观察发现：三个函数的图象都是双曲线，且分别关于直线
、
、
对称：三个函数解析式中分式部分完全相同，则图象的大小和形状完全相同，只有位置和对称轴发生了变化．因此，我们可以通过描点或平移的方法画函数图象．平移函数的图象可以得到函数、的图象，分别写出平移的方向和距离．
（2）探索思考：在所给的平面直角坐标系中，请用你喜欢的方法画出函数
图象，并写出这个函数的一条性质．
（3）拓展应用：若直线
过点
、
，结合你所画的函数图象，直接写出不等式
的解集．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H，给出下列结论：①BE=2AE；②△DFP∽△BPH；③△PFD∽△PDB；④DP2=PHPC
其中正确的是（ ）
A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线经过点O（0，0）与点A（4，0），顶点为点P，且最小值为-2．
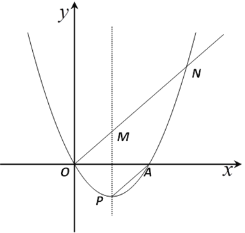
（1）求抛物线的表达式；
（2）过点O作PA的平行线交抛物线对称轴于点M，交抛物线于另一点N，求ON的长；
（3）抛物线上是否存在一个点E，过点E作x轴的垂线，垂足为点F，使得△EFO∽△AMN，若存在，试求出点E的坐标；若不存在请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，抛物线
与x轴交于A、B两点(点A在x轴的负半轴)，与y轴交于点C
． 抛物线的对称轴交抛物线于点D，交x轴于点E，点P是线段DE上一动点(点P不与DE两端点重合)，连接PC、PO．
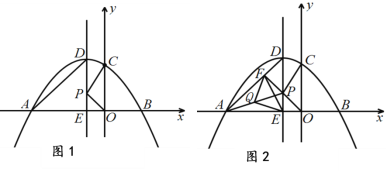
(1) 求抛物线的解析式和对称轴；
(2) 求∠DAO的度数和△PCO的面积；
(3) 在图1中，连接PA，点Q 是PA 的中点．过点P作PF⊥AD于点F，连接QE、QF、EF得到图2．试探究: 是否存在点P，使得
，若存在，请求点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某区域平面示意图如图，点O在河的一侧，AC和BC表示两条互相垂直的公路．甲勘测员在A处测得点O位于北偏东45°，乙勘测员在B处测得点O位于南偏西73.7°，测得AC=840m，BC=500m．请求出点O到BC的距离．参考数据：sin73.7°≈
，cos73.7°≈
，tan73.7°≈
查看答案和解析>>
科目：初中数学 来源： 题型：
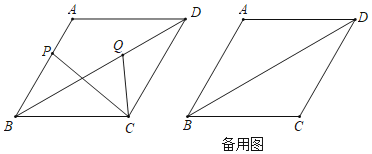
【题目】已知菱形ABCD中，AB＝4，∠BAD＝120°，点P是直线AB上任意一点，连接PC，在∠PCD内部作射线CQ与对角线BD交于点Q（与B、D不重合），且∠PCQ＝30°．
（1）如图，当点P在边AB上，且BP＝3时，求PC的长；
（2）当点P在射线BA上，且BP＝n（0≤n＜8）时，求QC的长；（用含n的式子表示）
（3）连接PQ，直线PQ与直线BC相交于点E，如果△QCE与△BCP相似，请直接写出线段BP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
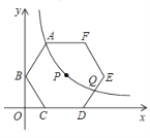
【题目】如图，在平面直角坐标系中，正六边形
的对称中心
在反比例函数
的图象上，边
在
轴上，点
在
轴上，已知
．若该反比例函数图象与
交于点
，则点的横坐标是_________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
