
【题目】如图1,抛物线![]() 与x轴交于A、B两点(点A在x轴的负半轴),与y轴交于点C
与x轴交于A、B两点(点A在x轴的负半轴),与y轴交于点C![]() . 抛物线的对称轴交抛物线于点D,交x轴于点E,点P是线段DE上一动点(点P不与DE两端点重合),连接PC、PO.
. 抛物线的对称轴交抛物线于点D,交x轴于点E,点P是线段DE上一动点(点P不与DE两端点重合),连接PC、PO.
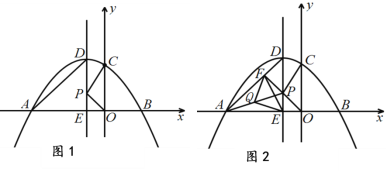
(1) 求抛物线的解析式和对称轴;
(2) 求∠DAO的度数和△PCO的面积;
(3) 在图1中,连接PA,点Q 是PA 的中点.过点P作PF⊥AD于点F,连接QE、QF、EF得到图2.试探究: 是否存在点P,使得![]() ,若存在,请求点P的坐标;若不存在,请说明理由.
,若存在,请求点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;
;![]() ;(2)45°;
;(2)45°;![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)把C点坐标代入![]() 解出解析式,再根据对称轴
解出解析式,再根据对称轴![]() 即可解出.
即可解出.
(2)把A、D、E、C点坐标求出后,因为AE=DE,且DE⊥AE,所以∠DAO=![]() ,P点y轴的距离等于OE,即可算出△POC的面积.
,P点y轴的距离等于OE,即可算出△POC的面积.
(3)设出PE=m,根据勾股定理用m表示出PA,根据直角三角形斜边中线是斜边的一半可以证明AQ=FQ=QE=QP,所以△AQF和△AQE都是等腰三角形,又因为∠DAO=![]() ,再根据角的关系可以证明△FEQ是等腰直角三角形,再根据
,再根据角的关系可以证明△FEQ是等腰直角三角形,再根据![]() ,解出m即可.可以通过圆的性质,来判断△FEQ是等腰直角三角形,再根据
,解出m即可.可以通过圆的性质,来判断△FEQ是等腰直角三角形,再根据![]() 建立等式算出m即可.
建立等式算出m即可.
解: (1) 将C![]() 代入
代入![]() 求得a=
求得a=![]() ,
,
∴抛物线的解析式为![]() ;
;
由![]() 可求抛物线的对称轴为直线
可求抛物线的对称轴为直线![]()
(2) 由抛物线可求一些点的坐标: ![]()
∴ AE=DE=3,又DE⊥AE
∴△ADE是等腰直角三角形 ∴∠DAO=45°
作PM⊥y轴于M,在对称轴上的点P的横坐标为-1,∴PM=1,又OP=![]()
∴△OPC的面积为![]()
(3)解:存在点![]() 满足题目条件.
满足题目条件.
解法一: 设点P的纵坐标为m(0<m<3),则PE=m,
∵点Q是PA的中点,∴QE、QF分别是Rt△PAE、Rt△PAF的公共斜边PA上的中线
∴QE=QF=AQ=PQ=![]()
∵QE=AQ,QF=AQ ∴∠EAQ=∠AEQ,∠FAQ=∠AFQ
∴∠EQP=2∠EAQ,∠FQP=2∠FAQ
∴∠EQF=2(∠EAQ + ∠FAQ ) =2∠DAO=90°
又∴QE=QF ∴△EFQ是等腰直角三角形
∴△EFQ的面积为![]()
由![]() 得
得![]() 解得
解得![]()
∵0<m<3 ∴![]() ∴在抛物线对称轴上的点P的坐标为
∴在抛物线对称轴上的点P的坐标为![]()
解法二: 设点P的纵坐标为m(0<m<3),则PE=m,![]()
∵点Q是PA的中点,∴QE、QF分别是Rt△PAE、Rt△PAF的公共斜边PA上的中线
∴QE=QF=AQ=PQ=![]()
∴四边形PEAF内接于半径为QE的⊙Q,
∴∠EQF=2∠DAO=90°
又∴QE=QF ∴△EFQ是等腰直角三角形
∴△EFQ的面积为![]()
由![]() 得
得![]() 解得
解得![]()
∵0<m<3 ∴![]() ∴在抛物线对称轴上的点P的坐标为
∴在抛物线对称轴上的点P的坐标为![]()


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
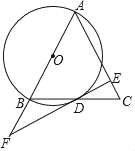
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)已知AB=4,AE=3.求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
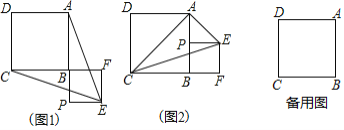
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上,如图2,当点P为AB的中点时,判断△ACE的形状,并说明理由;
(3)在(1)的条件下,将正方形ABCD固定,正方形BPEF绕点B旋转一周,设AB=4,BP=a,若在旋转过程中△ACE面积的最小值为4,请直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
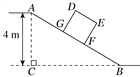
【题目】如图,某仓储中心有一斜坡AB,其坡比为i=1∶2,顶部A处的高AC为4 m,B,C在同一水平面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5 m,EF=2 m.将货柜沿斜坡向上运送,当BF=3.5 m时,求点D离地面的高.(![]() ≈2.236,结果精确到0.1 m)
≈2.236,结果精确到0.1 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面30°角的方向击出时,小球的飞行路线是一段抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系式为h=20t-![]()
![]() (t≥0). 回答问题:
(t≥0). 回答问题:

(1)小球的飞行高度能否达到19.5m;
(2) 小球从最高点到落地需要多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
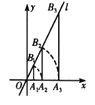
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作不轴的垂线交直
作不轴的垂线交直![]() 于点
于点![]() 以原点
以原点![]() 为圆心,
为圆心,![]() 的长为半径断弧交
的长为半径断弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;…按此作法进行下去,则
;…按此作法进行下去,则![]() 的长是____________.
的长是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式
,求代数式![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() 即
即![]()
∴![]() ∴
∴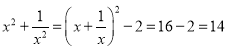
材料二:在解决某些连等式问题时,通常可以引入参数“![]() ”,将连等式变成几个值为
”,将连等式变成几个值为![]() 的等式,这样就可以通过适当变形解决问题.
的等式,这样就可以通过适当变形解决问题.
例:若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:令![]() 则
则![]() ,
,![]() ,
,![]() ,∴
,∴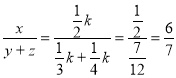
根据材料回答问题:
(1)已知![]() ,求
,求![]() 的值.
的值.
(2)已知![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com