
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式
,求代数式![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() 即
即![]()
∴![]() ∴
∴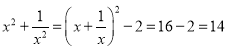
材料二:在解决某些连等式问题时,通常可以引入参数“![]() ”,将连等式变成几个值为
”,将连等式变成几个值为![]() 的等式,这样就可以通过适当变形解决问题.
的等式,这样就可以通过适当变形解决问题.
例:若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:令![]() 则
则![]() ,
,![]() ,
,![]() ,∴
,∴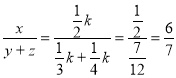
根据材料回答问题:
(1)已知![]() ,求
,求![]() 的值.
的值.
(2)已知![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于A、B两点(点A在x轴的负半轴),与y轴交于点C
与x轴交于A、B两点(点A在x轴的负半轴),与y轴交于点C![]() . 抛物线的对称轴交抛物线于点D,交x轴于点E,点P是线段DE上一动点(点P不与DE两端点重合),连接PC、PO.
. 抛物线的对称轴交抛物线于点D,交x轴于点E,点P是线段DE上一动点(点P不与DE两端点重合),连接PC、PO.
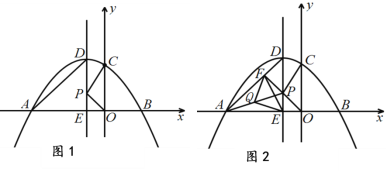
(1) 求抛物线的解析式和对称轴;
(2) 求∠DAO的度数和△PCO的面积;
(3) 在图1中,连接PA,点Q 是PA 的中点.过点P作PF⊥AD于点F,连接QE、QF、EF得到图2.试探究: 是否存在点P,使得![]() ,若存在,请求点P的坐标;若不存在,请说明理由.
,若存在,请求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的屋顶,是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中,AB=AC,测得BC=20米,∠C=41°,求顶点A到BC边的距离是多少米?(结果精确到0.1米.参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869.)
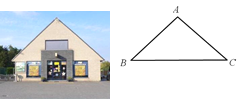
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推动实施健康中国战略,树立国家健康形象.手机APP推出多款健康运动软件,如“微信运动”.王老师随机调查了我校50名教师某日“微信运动”中的步数,并进行统计整理,绘制了如下的统计图表.
步数 | 频数 | 频率 |
| 8 |
|
| 15 | 0.3 |
|
| 0.24 |
| 10 | 0.2 |
| 3 | 0.06 |
| 2 | 0.04 |
合计 | 50 |
|
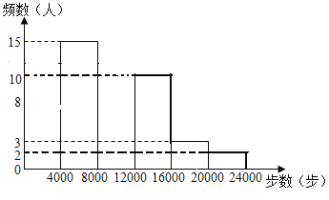
请根据以上信息,解答下列问题:
(1)![]() _______,
_______,![]() _______,
_______,![]() ________;
________;
(2)补全频数分布直方图;
(3)若某人一天的走路步数不低于16000步,将被“微信运动”评为“运动达人”.我市市区约有4000名初中教师,根据此项调查请估计市区被评为“运动达人”教师有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
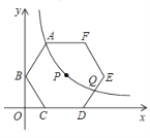
【题目】如图,在平面直角坐标系中,正六边形![]() 的对称中心
的对称中心![]() 在反比例函数
在反比例函数![]() 的图象上,边
的图象上,边![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,已知
轴上,已知![]() .若该反比例函数图象与
.若该反比例函数图象与![]() 交于点
交于点![]() ,则点的
,则点的![]() 横坐标是_________.
横坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD是平行四边形对角线AC,BD相交于点O,直线EF过点O,分别交AD,BC于点E,F.
(1)求证:AE=CF.
(2)如图2,若ABCD是老张家的一块平行四边形田地。P为水井,现要把这块田地平均分给两个儿子,为了用水方便,要求分给两个儿子的田地都与水井P相邻。请你帮老张家设计一下,画出图形,并说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列有规律的算式:13=1,13+23=9,13+23+33=36,13+23+33+43=100,13+23+33+43+53=225,…,探究并运用其规律计算:113+123+133+143+153+163+173+183+193+203的结果可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,消毒液、口罩成为了咱们的生活必需品.淘宝某医用器械药房推出![]() 种口罩进行销售,医用一次性口罩
种口罩进行销售,医用一次性口罩![]() 元
元![]() 个,医用外科口罩
个,医用外科口罩![]() 元
元![]() 个.
个.
(1)学校为做好开学复课准备,提前购进两种口罩![]() 个,共花费
个,共花费![]() 元,请问学校购买医用外科口罩多少个?
元,请问学校购买医用外科口罩多少个?
(2)因为![]() 月份疫情逐渐过去,各地开始复工复产,口罩的市场需求量依旧旺盛,该药房决定用
月份疫情逐渐过去,各地开始复工复产,口罩的市场需求量依旧旺盛,该药房决定用![]() 元再次购进一批口罩进行销售.医用一次性口罩
元再次购进一批口罩进行销售.医用一次性口罩![]() 个
个![]() 盒,每盒
盒,每盒![]() 元,医用外科口罩
元,医用外科口罩![]() 个
个![]() 盒,每盒
盒,每盒![]() 元.要求购进的医用外科口罩个数不超过医用一次性口罩的
元.要求购进的医用外科口罩个数不超过医用一次性口罩的![]() 倍,但不低于医用一次性口罩的
倍,但不低于医用一次性口罩的![]() 倍.若这批口罩全部销售完毕,为使获利最大,该药房应如何进货?最大获利为多少元?
倍.若这批口罩全部销售完毕,为使获利最大,该药房应如何进货?最大获利为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,点D在AB的延长线上,且∠BCD![]() ∠A.
∠A.
(1)求证:CD是⊙O的切线;
(2)若AC![]() 2,AB
2,AB![]()
![]() CD,求⊙O半径.
CD,求⊙O半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com