
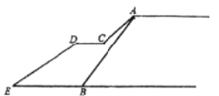
【题目】如图1,ABCD是平行四边形对角线AC,BD相交于点O,直线EF过点O,分别交AD,BC于点E,F.
(1)求证:AE=CF.
(2)如图2,若ABCD是老张家的一块平行四边形田地。P为水井,现要把这块田地平均分给两个儿子,为了用水方便,要求分给两个儿子的田地都与水井P相邻。请你帮老张家设计一下,画出图形,并说明理由?

【答案】(1)见解析;(2)图和理由见解析
【解析】
(1)利用ASA可证△AOE≌△COF,从而得出AE=CF;
(2)图形设计如下,根据平行四边形的特点,过对角线的交点O的直线可以将平行四边形分为2块面积相等部分,故只需要直线过点O和点P即可.
证明:(1)∵四边形ABCD是平行四边形
∴AD∥BC,OA=OC,
∴![]() DAC=
DAC=![]() BCA
BCA
在△AOE和△COF
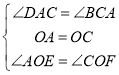
∴△AOE≌△COF(ASA),
∴AE=CF
(2)设计图形如下
理由:平行四边形是中心对称图形,对称中心是两条对角线的交点,只要满足两块地面积相等,且都与水井相邻就可以。那么可以考虑平行四边形的性质(平行四边形的对角线互相平分)来解题,找到对角线的交点与水井点P的连线的所在直线即可.


科目:初中数学 来源: 题型:
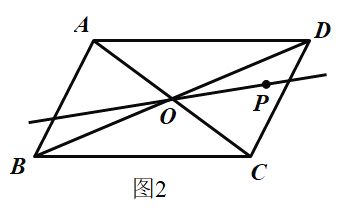
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作不轴的垂线交直
作不轴的垂线交直![]() 于点
于点![]() 以原点
以原点![]() 为圆心,
为圆心,![]() 的长为半径断弧交
的长为半径断弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;…按此作法进行下去,则
;…按此作法进行下去,则![]() 的长是____________.
的长是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
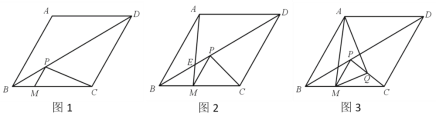
【题目】已知菱形ABCD中,∠ABC=60°,AB=4,点M在BC边上,过点M作PM∥AB交对角线BD于点P,连接PC.
(1)如图1,当BM=1时,求PC的长;
(2)如图2,设AM与BD交于点E,当∠PCM=45°时,求证:![]() =
=![]() ;
;
(3)如图3,取PC的中点Q,连接MQ,AQ.
①请探究AQ和MQ之间的数量关系,并写出探究过程;
②△AMQ的面积有最小值吗?如果有,请直接写出这个最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是重庆轻轨10号线龙头寺公园站入口扶梯建设示意图.起初工程师计划修建一段坡度为3:2的扶梯![]() ,扶梯总长为
,扶梯总长为![]() 米.但这样坡度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建
米.但这样坡度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建![]() 、
、![]() 两段扶梯,并减缓各扶梯的坡度,其中扶梯
两段扶梯,并减缓各扶梯的坡度,其中扶梯![]() 和平台
和平台![]() 形成的
形成的![]() 为135°,从
为135°,从![]() 点看
点看![]() 点的仰角为36.5°,
点的仰角为36.5°,![]() 段扶梯长
段扶梯长![]() 米,则
米,则![]() 段扶梯长度约为( )米(参考数据:
段扶梯长度约为( )米(参考数据:![]() ,
,![]() ,
,![]() )
)
A.43B.45C.47D.49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式
,求代数式![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() 即
即![]()
∴![]() ∴
∴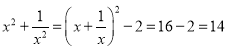
材料二:在解决某些连等式问题时,通常可以引入参数“![]() ”,将连等式变成几个值为
”,将连等式变成几个值为![]() 的等式,这样就可以通过适当变形解决问题.
的等式,这样就可以通过适当变形解决问题.
例:若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:令![]() 则
则![]() ,
,![]() ,
,![]() ,∴
,∴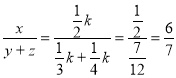
根据材料回答问题:
(1)已知![]() ,求
,求![]() 的值.
的值.
(2)已知![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,二次函数y=ax2+bx+c的图象经过点A(6,0),B(﹣2,0),C(0,4).
(1)求二次函数y=ax2+bx+c的表达式;
(2)点P在第一象限的抛物线上,且能够使△ACP得面积最大,求点P的坐标;
(3)在(2)的前提下,在抛物线的对称轴上是否存在点Q,使得△APQ为直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.
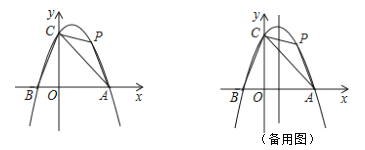
查看答案和解析>>
科目:初中数学 来源: 题型:
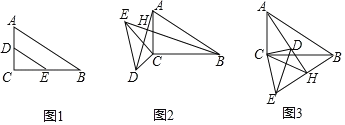
【题目】已知:已知Rt△ABC中,∠ACB=90°,D、E分别是AC、BC上的点,连DE,且![]() ,tanB
,tanB![]() ,如图1.
,如图1.
(1)如图2,将△CDE绕C点旋转,连AD、BE交于H,求证:AD⊥BE;
(2)如图3,当△CDE绕C点旋转过程中,当CH![]() 时,求
时,求![]() AH﹣BH的值;
AH﹣BH的值;
(3)若CD=1,当△CDE绕C点旋转过程中,直接写出AH的最大值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全体同学参加了“关怀贫困学生”爱心捐款活动,该校随机抽查了七、八、九三个年级部分学生捐款情况,将结果绘制成两幅不完整的统计图.根据图中的信息,解决下列问题:
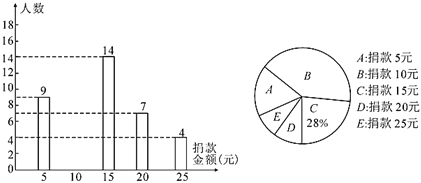
(1)这次共抽查了_______名学生进行统计,其中![]() 类所对应扇形的圆心角的度数为________;
类所对应扇形的圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校有![]() 名学生,估计该校捐款
名学生,估计该校捐款![]() 元的学生有多少人?
元的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
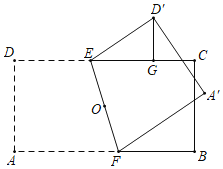
【题目】如图,点O是矩形ABCD的对角线的交点,AB=15,BC=8,直线EF经过点O,分别与边CD,AB相交于点E,F(其中0<DE<![]() ).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是_____,此时折痕EF的长为_____.
).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是_____,此时折痕EF的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com