
【题目】如图,在平面直角坐标中,二次函数y=ax2+bx+c的图象经过点A(6,0),B(﹣2,0),C(0,4).
(1)求二次函数y=ax2+bx+c的表达式;
(2)点P在第一象限的抛物线上,且能够使△ACP得面积最大,求点P的坐标;
(3)在(2)的前提下,在抛物线的对称轴上是否存在点Q,使得△APQ为直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.
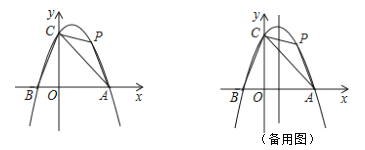
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)P(3,5);(3)点Q坐标为(2,﹣
x+4;(2)P(3,5);(3)点Q坐标为(2,﹣![]() )或(2,
)或(2,![]() )或(2,1)或(2,4)
)或(2,1)或(2,4)
【解析】
(1)将A、B、C三点代入,可求得抛物线的解析式;
(2)设P(m,﹣![]() m2+
m2+![]() m+4),先求出AC的解析式,从而得出点E的坐标,进而得出PE的长,从而求得用m表示的△PCA的面积,最后根据二次函数的特点,求出最值;
m+4),先求出AC的解析式,从而得出点E的坐标,进而得出PE的长,从而求得用m表示的△PCA的面积,最后根据二次函数的特点,求出最值;
(3)设设点Q的坐标为(2,m),根据平面直角坐标系中任意两点之间的距离公式求出AQ2、PQ2和AP2,存在3种情况,一种是∠QAP=90°,第二种是∠AQP=90°,第三种是∠QPA=90°时,利用勾股定理分别求解即可.
解:(1)把A(6,0),B(﹣2,0),C(0,4)的坐标代入y=ax2+bx+c,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4.
x+4.
(2)作PE∥OC交AC于E.
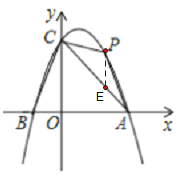
设P(m,﹣![]() m2+
m2+![]() m+4).
m+4).
设直线AC的解析式为y=kx+d
将点A和点C的坐标代入,得
![]()
解得: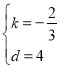
∴直线AC的解析式为y=﹣![]() x+4,
x+4,
∴E(m,﹣![]() m+4),
m+4),
∴PE=﹣![]() m2+2m,
m2+2m,
∴S△PAC=![]() ×(﹣
×(﹣![]() m2+2m)×6=﹣m2+6m=﹣(m﹣3)2+9,
m2+2m)×6=﹣m2+6m=﹣(m﹣3)2+9,
∵﹣1<0,
∴m=3时,△PAC的面积最大,
∴P(3,5).
(3)∵A(6,0),P(3,5),抛物线y=﹣![]() x2+
x2+![]() x+4的对称轴为直线x=2
x+4的对称轴为直线x=2
∴可设点Q的坐标为(2,m)
∴AQ2=![]()
![]()
PQ2=![]()
![]()
AP2=![]()
①当∠QAP=90°时,则AQ2+AP2= PQ2
即![]() +34=
+34=![]()
解得:m=![]()
∴Q(2,![]() )
)
②当∠AQP=90°时,则AQ2+PQ2= AP2
即![]() +
+![]() =34
=34
解得:m1=1,m2=4
∴Q(2,1)或(2,4)
③当∠QPA=90°时,则AP2+PQ2= AQ2
即34+![]() =
=![]()
解得:m=![]()
∴Q(2,![]() )
)
综上所述,满足条件的点Q坐标为(2,![]() )或(2,
)或(2,![]() )或(2,1)或(2,4).
)或(2,1)或(2,4).


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
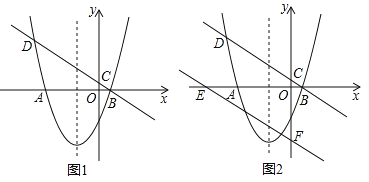
【题目】如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直线y=kx+![]() 分别与y轴及抛物线交于点C,D.
分别与y轴及抛物线交于点C,D.
(1)求直线和抛物线的表达式;
(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;
(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
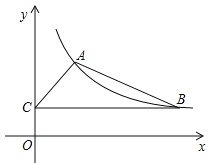
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐高积木是儿童喜爱的玩具.这种塑胶积木一头有凸粒,另一头有可嵌入凸粒的孔,形状有1300多种,每一种形状都有12种不同的颜色,以红、黄、蓝、白、绿色为主.它靠小朋友自己动手动脑,可以拼插出变化无穷的造型,令人爱不释手,被称为“魔术塑料积木”.某玩具店购进一批甲、乙两款乐高积木,它们的进货单价之和是720元.甲款积木零售单价比进货单价多80元.乙款积木零售价比进货单价的1.5倍少120元,按零售单价购买甲款积木4盒和乙款积木2盒,共需要2640元.
(1)分别求出甲乙两款积木的进价;
(2)该玩具店平均一个星期卖出甲款积木40盒和乙款积木24盒,经调查发现,甲款积木零售单价每降低2元,平均一个星期可多售出甲款积木4盒,商店决定把甲款积木的零售价下降![]() 元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当
元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当![]() 为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD是平行四边形对角线AC,BD相交于点O,直线EF过点O,分别交AD,BC于点E,F.
(1)求证:AE=CF.
(2)如图2,若ABCD是老张家的一块平行四边形田地。P为水井,现要把这块田地平均分给两个儿子,为了用水方便,要求分给两个儿子的田地都与水井P相邻。请你帮老张家设计一下,画出图形,并说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
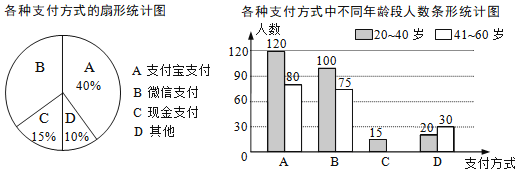
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
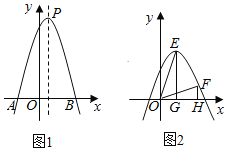
【题目】如图1,已知抛物线y=ax2+bx+c的顶点为P(1,9),与x轴的交点为A(﹣2,0),B.
(1)求抛物线的解析式;
(2)M为x轴上方抛物线上的一点,MB与抛物线的对称轴交于点C,若∠COB=2∠CBO,求点M的坐标;
(3)如图2,将原抛物线沿对称轴平移后得到新抛物线为y=ax2+bx+h,E,F新抛物线在第一象限内互不重合的两点,EG⊥x轴,FH⊥x轴,垂足分别为G,H,若始终存在这样的点E,F,满足△GEO≌△HOF,求h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
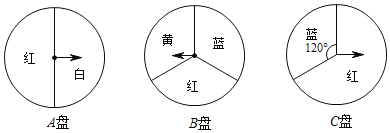
【题目】小颖为学校联欢会设计了一个“配紫色”游戏:如图是三个可以自由转动的转盘,A盘和B盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)若游戏者同时转动A盘和B盘,请利用画树状图或列表的方法,求他获胜的概率;
(2)若游戏者同时转动B盘和C盘,请直接写出他获胜的概率,不必写出求解过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com