
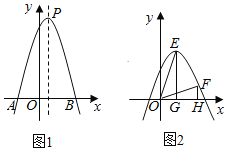
【题目】如图1,已知抛物线y=ax2+bx+c的顶点为P(1,9),与x轴的交点为A(﹣2,0),B.
(1)求抛物线的解析式;
(2)M为x轴上方抛物线上的一点,MB与抛物线的对称轴交于点C,若∠COB=2∠CBO,求点M的坐标;
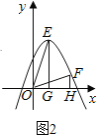
(3)如图2,将原抛物线沿对称轴平移后得到新抛物线为y=ax2+bx+h,E,F新抛物线在第一象限内互不重合的两点,EG⊥x轴,FH⊥x轴,垂足分别为G,H,若始终存在这样的点E,F,满足△GEO≌△HOF,求h的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设该抛物线解析式为![]() ,将点
,将点![]() 的坐标代入求得
的坐标代入求得![]() 的值即可;
的值即可;
(2)作原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() ,结合三角形外角定理推知
,结合三角形外角定理推知![]() ,故
,故![]() .由勾股定理求得线段
.由勾股定理求得线段![]() 的长度,则
的长度,则![]() .由待定系数法确定直线
.由待定系数法确定直线![]() 解析式为
解析式为![]() ,与抛物线
,与抛物线![]() 联立得到:
联立得到:![]() .由此求得点
.由此求得点![]() 坐标;
坐标;
(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,由全等三角形的对应边相等和二次函数图象上点的坐标特征建立
,由全等三角形的对应边相等和二次函数图象上点的坐标特征建立![]() 与
与![]() 或
或![]() 的函数关系式,从而求
的函数关系式,从而求![]() 的取值范围.
的取值范围.
解:(1)![]() 抛物线
抛物线![]() 的顶点为
的顶点为![]() ,
,
![]() 设该抛物线解析式为
设该抛物线解析式为![]() ,
,
把![]() 代入抛物线解析式得
代入抛物线解析式得![]() ,
,![]() ,
,
![]() ;
;
(2)令![]() 得
得![]() ,
,![]() ,或
,或![]() ,
,
![]() ,
,
![]()
抛物线对称轴直线![]() 与
与![]() 轴交点为
轴交点为![]() ,
,
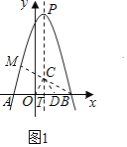
如图1,作原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]() 设直线
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,
解得![]() ,
,![]() .
.
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
与抛物线![]() 联立得
联立得![]() .
.
![]()
![]() ,
,![]() .
.
![]()
![]() ,
,
故点![]() 坐标为
坐标为![]() ;
;
(3)如图2,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设新抛物线解析式为![]() ,
,
把点![]() ,
,![]() 的坐标代入抛物线的解析式得:
的坐标代入抛物线的解析式得:![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 且
且![]()
把![]() 代入
代入![]() ,得
,得![]() .
.
![]() 且
且![]() .
.
![]()
![]() .
.
故![]() 的取值范围
的取值范围![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
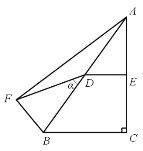
【题目】如图,Rt△ABC中,∠C=90°,BC=6,DE是△ABC的中位线,点D在AB上,把点B绕点D按顺时针方向旋转α(0°<α<180°)角得到点F,连接AF,BF.下列结论:①△ABF是直角三角形;②若△ABF和△ABC全等,则α=2∠BAC或2∠ABC;③若α=90°,连接EF,则S△DEF=4.5;其中正确的结论是( )
A.①②B.①③C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,二次函数y=ax2+bx+c的图象经过点A(6,0),B(﹣2,0),C(0,4).
(1)求二次函数y=ax2+bx+c的表达式;
(2)点P在第一象限的抛物线上,且能够使△ACP得面积最大,求点P的坐标;
(3)在(2)的前提下,在抛物线的对称轴上是否存在点Q,使得△APQ为直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.
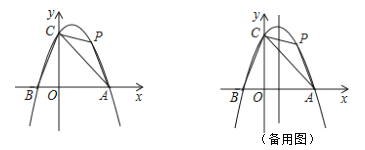
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,附中初![]() 级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
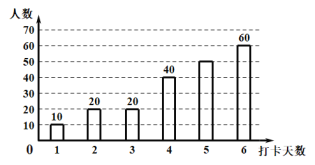
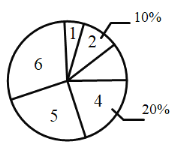
通过分析上面![]() 个统计图,制作如下表格:
个统计图,制作如下表格:
统计量 | 平均数 | 中位数 | 众数 |
天数 | 4.4 | a | b |
(1)填空:![]() _______,
_______,![]() _______,并补全条形统计图.
_______,并补全条形统计图.
(2)因为疫情期间,在家体育锻炼条件受限,所以规定坚持打卡不低于![]() 天即为合格.初
天即为合格.初![]() 级共有学生
级共有学生![]() 人,请你估计初
人,请你估计初![]() 级学生中体育锻炼合格的人数.
级学生中体育锻炼合格的人数.
(3)若统计时漏掉![]() 名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学全体同学参加了“关怀贫困学生”爱心捐款活动,该校随机抽查了七、八、九三个年级部分学生捐款情况,将结果绘制成两幅不完整的统计图.根据图中的信息,解决下列问题:
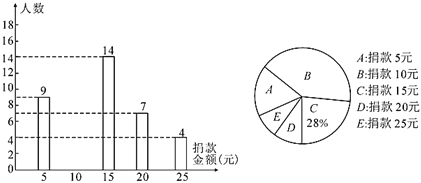
(1)这次共抽查了_______名学生进行统计,其中![]() 类所对应扇形的圆心角的度数为________;
类所对应扇形的圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校有![]() 名学生,估计该校捐款
名学生,估计该校捐款![]() 元的学生有多少人?
元的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题:
(1)求本次调查中共抽取的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,阅读![]() 本书籍的人数所在扇形的圆心角度数是 ;
本书籍的人数所在扇形的圆心角度数是 ;
(4)若该校有![]() 名学生,估计该校在这次活动中阅读书籍的数量不低于
名学生,估计该校在这次活动中阅读书籍的数量不低于![]() 本的学生有多少人?
本的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止,设P、Q同时出发t秒时,BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示(其中曲线OG为抛物线的一部分,其余各部分均为线段)所示,则下列结论:①BEBC;②当t6秒时,ABE PQB;③点P运动了18秒;④当t![]() 秒时,ABE∽QBP.其中正确的是( ).
秒时,ABE∽QBP.其中正确的是( ).
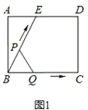
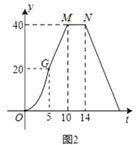
A.①②B.①③④C.③④D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com