
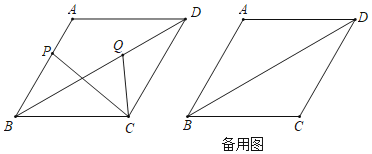
【题目】已知菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,连接PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上,且BP=3时,求PC的长;
(2)当点P在射线BA上,且BP=n(0≤n<8)时,求QC的长;(用含n的式子表示)
(3)连接PQ,直线PQ与直线BC相交于点E,如果△QCE与△BCP相似,请直接写出线段BP的长.
【答案】(1)![]() ;(2)QC=
;(2)QC=![]() (0≤n<8);(3)BP的值为2+2
(0≤n<8);(3)BP的值为2+2![]() 或2
或2![]() ﹣2.
﹣2.
【解析】
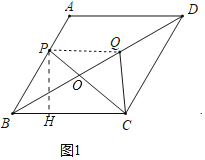
(1)如图1中,作PH⊥BC于H.解直角三角形求出BH,PH,在Rt△PCH中,由勾股定理即可得出答案.
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.证明△POQ∽△BOC,推出∠OPQ=∠OBC=30°=∠PCQ,推出PQ=CQ,推出PC=![]() CQ,在Rt△PHB中,BH=
CQ,在Rt△PHB中,BH=![]() n,PH=
n,PH=![]() n,根据PC2=PH2+CH2,可得结论.
n,根据PC2=PH2+CH2,可得结论.
(3)分三种情形:①如图2中,若直线QP交直线BC于B点左侧的点E.②如图3中,若直线QP交直线BC于C点右侧的点E.③如图4中,当点P在AB的延长线上时,由相似三角形的性质分别求解即可.
解:(1)如图1中,作PH⊥BC于H.
∵四边形ABCD是菱形,
∴AB=BC=4,AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=120°,
∴∠PBH=60°,
∵PB=3,∠PHB=90°,
∴BH=PBcos60°=![]() ,PH=PBsin60°=
,PH=PBsin60°=![]() ,
,
∴CH=BC﹣BH=4﹣![]() =
=![]() ,
,
∴PC═![]() =
=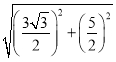 =
=![]() .
.
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.
∵四边形ABCD是菱形,
∴∠ABD=
∵∠PCQ=30°,
∴∠PBO=∠QCO,
∵∠POB=∠QOC,
∴△POB∽△QOC,
∴![]() ,
,
∴![]() ,
,
∵∠POQ=∠BOC,
∴△POQ∽△BOC,
∴∠OPQ=∠OBC=30°=∠PCQ,
∴PQ=QC,
∴PC=![]() QC,
QC,
在Rt△PHB中,BP=n,
∴BH=![]() n,PH=
n,PH=![]() n,
n,
∵PC2=PH2+CH2,
∴3QC2=(![]() n)2+(4﹣
n)2+(4﹣![]() n)2,
n)2,
∴QC=![]() (0≤n<8).
(0≤n<8).
(3)①如图2中,若直线QP交直线BC于B点左侧的点E.
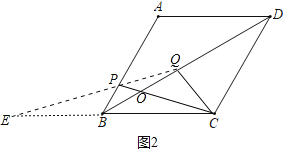
此时∠CQE=120°,
∵∠PBC=60°,
∴△PBC中,不存在角与∠CQE相等,
此时△QCE与△BCP不可能相似.
②如图3中,若直线QP交直线BC于点C右侧的点E.
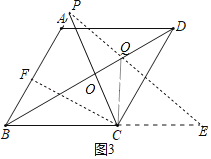
则∠CQE=∠B=QBC+∠QCP=60°=∠CBP,
∵∠PCB>∠E,
∴只可能∠BCP=∠QCE=75°,
作CF⊥AB于F,则BF=2,CF=2![]() ,∠PCF=45°,
,∠PCF=45°,
∴PF=CF=2![]() ,
,
此时BP=2+2![]() ,
,
③如图4中,当点P在AB的延长线上时,
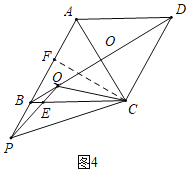
∵△CBE与△CBP相似,
∴∠CQE=∠CBP=120°,
∴∠QCE=∠CBP=15°,
作CF⊥AB于F.
∵∠FCB=30°,
∴∠FCB=45°,
∴BF=![]() BC=2,CF=PF=2
BC=2,CF=PF=2![]() ,
,
∴BP=2![]() ﹣2.
﹣2.
综上所述,满足条件的BP的值为2+2![]() 或2
或2![]() ﹣2.
﹣2.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形, ![]() 是一个格点三角形.
是一个格点三角形.
![]() 在图
在图![]() 中,请判断
中,请判断![]() 与
与![]() 是否相似,并说明理由;
是否相似,并说明理由;
![]() 在图
在图![]() 中,以O为位似中心,再画一个格点三角形,使它与
中,以O为位似中心,再画一个格点三角形,使它与![]() 的位似比为2:1
的位似比为2:1
![]() 在图
在图![]() 中,请画出所有满足条件的格点三角形,它与
中,请画出所有满足条件的格点三角形,它与![]() 相似,且有一条公共边和一个公共角.
相似,且有一条公共边和一个公共角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面30°角的方向击出时,小球的飞行路线是一段抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系式为h=20t-![]()
![]() (t≥0). 回答问题:
(t≥0). 回答问题:

(1)小球的飞行高度能否达到19.5m;
(2) 小球从最高点到落地需要多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点![]() ,以线段
,以线段![]() 为直径作圆,圆心为
为直径作圆,圆心为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 轴上任意一动点,连接
轴上任意一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() :
:
①当![]() 时,求所有
时,求所有![]() 点的坐标 (直接写出);
点的坐标 (直接写出);
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
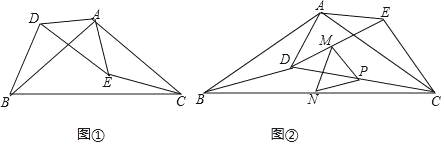
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,
上一点,![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的延长线上一点,且
的延长线上一点,且![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() 的半径为5,
的半径为5,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
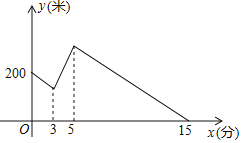
【题目】甲、乙两人分别从各自家出发乘坐出租车前往智博会,由于堵车,两人同时选择就近下车,已知甲车在乙车前面200米的A地下车,然后分别以各自的速度匀速走向会场,3分钟后,乙发现有物品遗落在出租车上,于是立即以不变的速度返回寻找,找到出租车时,出租车恰好向会场方向行驶了100米,乙拿到物品后立即以原速返回继续走向会场,同时甲以先前速度的一半走向会场,又经过10分钟,乙在B地追上甲,两人随后一起以甲放慢后的速度行走1分钟到达会场,甲、乙两人相距的路程y(m)与甲行走的时间x(min)之间的关系如图所示,(乙拿物品的时间忽略不计),则A地距离智博会会场的距离为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com