
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

【答案】(1)2(2)当点P、Q运动时,线段DE的长度不会改变。理由见解析
【解析】解:(1)∵△ABC是边长为6的等边三角形,∴∠ACB=60°。
∵∠BQD=30°,∴∠QCP=90°。
设AP=x,则PC=6﹣x,QB=x,∴QC=QB+C=6+x。
∵在Rt△QCP中,∠BQD=30°,∴PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),解得x=2。
(6+x),解得x=2。
∴当∠BQD=30°时,AP=2。
(2)当点P、Q运动时,线段DE的长度不会改变。理由如下:
作QF⊥AB,交直线AB的延长线于点F,连接QE,PF。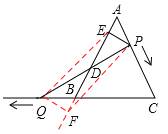
∵PE⊥AB于E,∴∠DFQ=∠AEP=90°。
∵点P、Q做匀速运动且速度相同,∴AP=BQ。
∵△ABC是等边三角形,∴∠A=∠ABC=∠FBQ=60°。
∴在△APE和△BQF中,
∵∠A=∠FBQ,AP=BQ,∠AEP=∠BFQ=90°,∴△APE≌△BQF(AAS)。
∴AE=BF,PE=QF且PE∥QF。∴四边形PEQF是平行四边形。
∴DE=![]() EF。
EF。
∵EB+AE=BE+BF=AB,∴DE=![]() AB。
AB。
又∵等边△ABC的边长为6,∴DE=3。
∴当点P、Q运动时,线段DE的长度不会改变。
(1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QCP=90°,设AP=x,则PC=6﹣x,QB=x,在Rt△QCP中,∠BQD=30°,PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),求出x的值即可。
(6+x),求出x的值即可。
(2)作QF⊥AB,交直线AB的延长线于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE=![]() AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变。
AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变。


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知三角形ABC在平面直角坐标系中的位置如图所示.将三角形ABC向右平移6个单位长度,再向下平移6个单位长度得到三角形A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的三角形A1B1C1;
(2)求三角形ABC的面积;
(3)直接写出三角形A1B1C1各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
编号 类型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读小强同学数学作业本上的截图内容并完成任务:
解方程组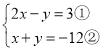
解:由①,得![]() ,③ 第一步
,③ 第一步
把③代入①,得![]() .第二步
.第二步
整理得,![]() .第三步
.第三步
因为![]() 可以取任意实数,所以原方程组有无数个解 第四步
可以取任意实数,所以原方程组有无数个解 第四步
任务:(1)这种解方程组的方法称为 ;
(2)利用此方法解方程组的过程中所体现的数学思想是 ;(请你填写正确选项)
A.转化思想 B.函数思想 C.数形结合思想 D.公理化思想
(3)小强的解法正确吗? (填正确或不正确),如果不正确,请指出错在第 步,请选择恰当的解方程组的方法解该方程组.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“百变魔方”社团准备购买![]() 两种魔方.已知购买
两种魔方.已知购买![]() 个
个![]() 种魔方和
种魔方和![]() 个
个![]() 种魔方共需
种魔方共需![]() 元;购买
元;购买![]() 个
个![]() 种魔方所需款数和购买
种魔方所需款数和购买![]() 个
个![]() 种魔方所需款数相同.优惠活动:活动一:“疯狂打折”:
种魔方所需款数相同.优惠活动:活动一:“疯狂打折”:![]() 种魔方八折,
种魔方八折,![]() 种魔方四折;活动二:“买一送一”:购买一个
种魔方四折;活动二:“买一送一”:购买一个![]() 种魔方送一个
种魔方送一个![]() 种魔方
种魔方
(1)求![]() 这两种魔方的单价;
这两种魔方的单价;
(2)结合社员们的需求,社团决定购买![]() 两种魔方共
两种魔方共![]() 个(其中
个(其中![]() 种魔方不超过
种魔方不超过![]() 个) .某商店有两种优惠活动,如图所示.设购买
个) .某商店有两种优惠活动,如图所示.设购买![]() 种魔方
种魔方![]() 个,按活动一购买所需费用为
个,按活动一购买所需费用为![]() 元,按活动二购买所需费用为
元,按活动二购买所需费用为![]() 元.请根据以上信息,解决以下问题:
元.请根据以上信息,解决以下问题:

①试用含![]() 的代数式分别表示
的代数式分别表示![]() .
.
②试求当购买![]() 种魔方多少个时,选择两种优惠活动同样实惠?
种魔方多少个时,选择两种优惠活动同样实惠?
③以![]() 种魔方的个数说明选择哪种优惠活动购买魔方更实惠.
种魔方的个数说明选择哪种优惠活动购买魔方更实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,BE⊥CD于点E,点F在AB上,且AF=CE,连接DF.
(1)求证:四边形BEDF是矩形;
(2)连接CF,若CF平分∠BCD,且CE=3,BE=4,求矩形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在用描点法画二次函数y=ax2+bx+c图象时,由于粗心,他算错了一个y值,列出了下面表格:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
(1)请指出这个错误的y值,并说明理由;
(2)若点M(a,y1),N(a+4,y2)在二次函数y=ax2+bx+c图象上,且a>﹣1,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() :y=2x+1与直线
:y=2x+1与直线 ![]() :y=mx+4相交于点P(1,b)
:y=mx+4相交于点P(1,b)
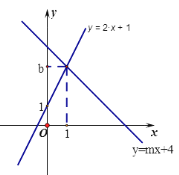
(1)求b,m的值
(2)垂直于x轴的直线 x=a与直线 ![]() ,
,![]() 分别相交于C,D,若线段CD长为2,求a的值
分别相交于C,D,若线段CD长为2,求a的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com