Question

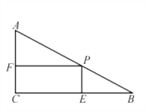
【题目】如图，在Rt△ABC中，∠C=90°,∠B=30°,AB=12cm，点P是AB边上的一个动点，过点P作PE⊥BC于点E,PF⊥AC于点F,当PB=6cm时，四边形PECF的面积最大，最大值为______

Answer 1

【答案】9cm2

【解析】试题分析：设PE=x，在Rt△PEB中，根据∠B=30°，可知PB=2x，BE=x，再在Rt△ABC中，利用三角函数的知识求出BC的长，进而可以表示出CE的长度；然后利用矩形的面积公式，即可得到四边形PECF的面积S关于x的表达式，对表达式进行配方，利用二次函数的最值即可得到答案.

解：设PE=x，由∠B=30°，

得PB=2x，BE=x.

由AB=12cm，

得BC=12×cos30°=6cm，

故CE=BC-BE=6－x.

则四边形PECF的面积=CE×PE=(6－x)x=－x2+6x=－ (x-3)2+9，

当x=3cm，即PB=2x=6cm时，四边形PECF的面积最大，最大值是9cm2.

故答案为：9cm2.