
【题目】如图,抛物线![]() 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)

(1)求该抛物线的解析式;
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
【答案】详见解析
【解析】
(1)利用待定系数法求出抛物线的解析式。
(2)首先求出△PCE面积的表达式,然后利用二次函数的性质求出其最大值。
(3)△OMD为等腰三角形,分DM=DO,MD=MO,OD=OM三种情况讨论即可。
解:(1)把点C(0,-4),B(2,0)分别代入![]() 中,
中,
得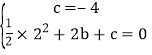 ,解得
,解得![]() 。
。
∴该抛物线的解析式为![]() 。
。
(2)令y=0,即![]() ,解得x1=-4,x2=2。
,解得x1=-4,x2=2。
∴A(﹣4,0),S△ABC=![]() ABOC=12。
ABOC=12。
设P点坐标为(x,0),则PB=2﹣x。
∵PE∥AC,∴∠BPE=∠BAC,∠BEP=∠BCA。∴△PBE∽△ABC。
∴![]() ,即
,即![]() ,化简得:
,化简得:![]() 。
。
∴![]()
![]() 。
。
∴当x=﹣1时,S△PCE的最大值为3。
(3)△OMD为等腰三角形,可能有三种情形:
①当DM=DO时,如图①所示,
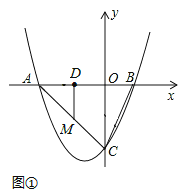
∵DO=DM=DA=2,
∴∠OAC=∠AMD=45°。∴∠ADM=90°。
∴M点的坐标为(-2,-2)。
②当MD=MO时,如图②所示,
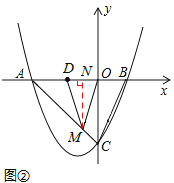
过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,AN=AD+DN=3,
又△AMN为等腰直角三角形,∴MN=AN=3。
∴M点的坐标为(-1,-3)。
③当OD=OM时,
∵△OAC为等腰直角三角形,
∴点O到AC的距离为![]() ×4=
×4=![]() ,即AC上的点与点O之间的最小距离为
,即AC上的点与点O之间的最小距离为![]() 。
。
∵![]() >2,∴OD=OM的情况不存在。
>2,∴OD=OM的情况不存在。
综上所述,点M的坐标为(-2,-2)或(-1,-3)。


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+4x-1与y轴交于点C,CD∥x轴交抛物线于另一点D,AB∥x轴交抛物线于点A,B,点A在点B的左侧,且两点均在第一象限,BH⊥CD于点H.设点A的横坐标为m.
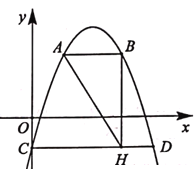
(1)当m=1时,求AB的长.
(2)若AH=![]() (CH-DH),求m的值.
(CH-DH),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、E在⊙O上,∠B=2∠ACE,在BA的延长线上有一点P,使得∠P=∠BAC,弦CE交AB于点F,连接AE.
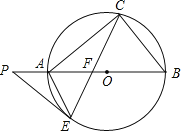
(1)求证:PE是⊙O的切线;
(2)若AF=2,AE=EF=![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发一种新的药物,据监测,如果成年人按规定的剂量服用,服药后2小时,每毫升血液中的含药量达到最大值,之后每毫升血液中的含药量逐渐衰减.若一次服药后每毫升血液中的含药量y(单位:微克)与服药后的时间t(单位:小时)之间近似满足某种函数关系,下表是y与t的几组对应值,其部分图象如图所示.
t | 0 | 1 | 2 | 3 | 4 | 6 | 8 | 10 | … |
y | 0 | 2 | 4 | 2.83 | 2 | 1 | 0.5 | 0.25 | … |
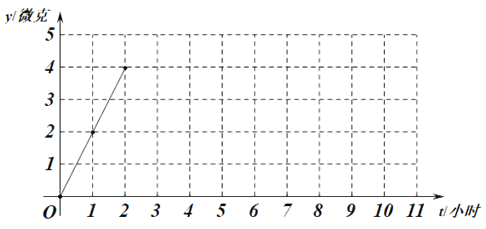
(1)在所给平面直角坐标系中,继续描出上表中已列出数值所对应的点(t,y),并补全该函数的图象;
(2)结合函数图象,解决下列问题:
①某病人第一次服药后5小时,每毫升血液中的含药量约为_______微克;若每毫升血液中含药量不少于0.5微克时治疗疾病有效,则第一次服药后治疗该疾病有效的时间共持续约_______小时;
②若某病人第一次服药后8小时进行第二次服药,第二次服药对血液中含药量的影响与第一次服药相同,则第二次服药后2小时,每毫升血液中的含药量约为_______微克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握我区中考模拟数学试题的命题质量与难度系数,命题教师选取一个水平相当的初三年级进行调研,将随机抽取的部分学生成绩(得分为整数,满分为130分)分为5组:第一组5570;第二组7085;第三组85100;第四组100115;第五组115130,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
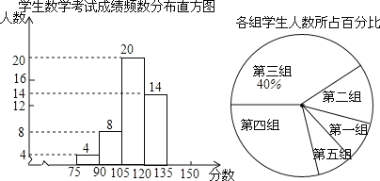
(1)本次调查共随机抽取了__ _名学生;
(2)补全频数分布直方图;
(3)将得分转化为等级,规定:得分低于70分评为“D”,70100分评为“C”,10011评为“B”,115130分评为“A”,根据目前的统计,请你估计全区该年级4500名考生中,考试成绩评为“B”级及其以上的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,∠ABC的平分线BF交AD于点F,交BC于点D.
(1)求证:BE=EF;
(2)若DE=4,DF=3,求AF的长.
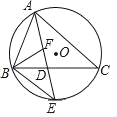
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
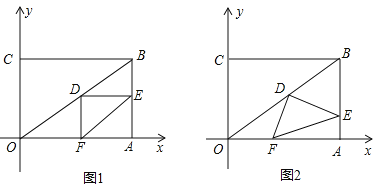
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣m)2+2(x﹣m)(m为常数)
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)当m取什么值时,该函数的图象关于y轴对称?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com