
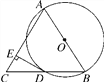
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.
【答案】(1)证明见解析(2)2![]()
【解析】【试题分析】(1)连接AD.利用中垂线的性质证明即可;(2)∵∠BAC=60°,由(1)知AB=AC,根据有一角是60°的等腰三角形是等边三角形,得:△ABC是等边三角形,根据等边三角形的性质得:∠C=60°.因为AB=2×4=8,则DC=![]() BC=
BC=![]() AB=4.又∵因为DE⊥AC,根据三角形函数解得:DE=DC·sinC=4·sin60°=2
AB=4.又∵因为DE⊥AC,根据三角形函数解得:DE=DC·sinC=4·sin60°=2![]() .
.
【试题解析】
(1)连接AD.∵AB是⊙O的直径,∴∠ADB=90°.∵DC=BD,∴AB=AC.
(2)∵∠BAC=60°,由(1)知AB=AC,∴△ABC是等边三角形,∴∠C=60°.
∵AB=2×4=8,∴DC=![]() BC=
BC=![]() AB=4.又∵DE⊥AC,∴DE=DC·sinC=4·sin60°=2
AB=4.又∵DE⊥AC,∴DE=DC·sinC=4·sin60°=2![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
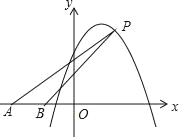
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(﹣5,0)、(﹣2,0).点P在抛物线y=﹣2x2+4x+8上,设点P的横坐标为m.当0≤m≤3时,△PAB的面积S的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)。
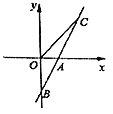
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△AOC =2,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
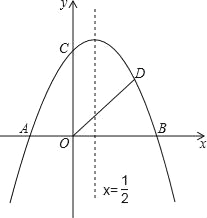
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=
x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=![]() ,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);
,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);
(1)求抛物线的解析式和点D的坐标;
(2)点M是抛物线上的动点,在x轴上存在一点N,使得A、D、M、N四个点为顶点的四边形是平行四边形,求出点M的坐标;
(3)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(-2,-1)在它的图像上 B. 它的图像在第一、三象限
C. 当![]() 时,y随x的增大而增大 D. 当
时,y随x的增大而增大 D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】C
【解析】试题分析:反比例函数![]() 的性质:当
的性质:当![]() 时,图象在一、三象限,在每一象限,y随x的增大而减小;当
时,图象在一、三象限,在每一象限,y随x的增大而减小;当![]() 时,图象在二、四象限,在每一象限,y随x的增大而增大.
时,图象在二、四象限,在每一象限,y随x的增大而增大.
A.点![]() 在它的图象上,B.它的图象在第一、三象限,C.当
在它的图象上,B.它的图象在第一、三象限,C.当![]() 时,
时,![]() 随
随![]() 的增大而减小,均正确,不符合题意;
的增大而减小,均正确,不符合题意;
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小,故错误,本选项符合题意.
的增大而减小,故错误,本选项符合题意.
考点:反比例函数的性质
点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.
【题型】单选题
【结束】
8
【题目】由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
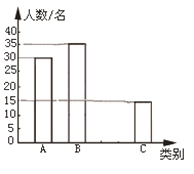
A. 900名 B. 1050名 C. 600名 D. 450名
查看答案和解析>>
科目:初中数学 来源: 题型:
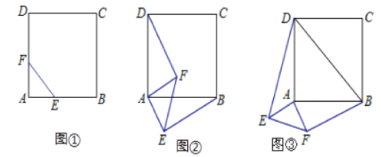
【题目】(1)如图①,正方形ABCD,点E、点F分别在AB和AD上,且AE=AF.此时,线段BE、DF的数量关系是 ,位置关系是 .请直接写出结论.
(2)如图②,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由。
(3)如图③,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB,得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
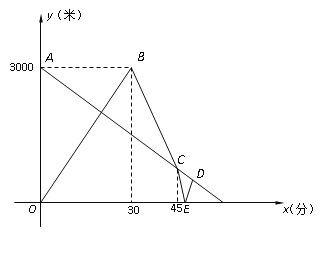
【题目】小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图像.
(注:小明和妈妈始终在同一条笔直的公路上行走,图像上A、C、D三点在一条直线上)
(1)求线段BC的函数表达式;
(2)求点D坐标;
(3)当 x的值为 时,小明与妈妈相距1 500米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个大于1的正整数n进行如下操作:
① 将n拆分为两个正整数a、b的和,并计算乘积a×b
② 对于正整数a、b分别重复此操作,得到另外两个乘积
③ 重复上述过程,直至不能再拆分为止(即拆分到正整数1)
当n=6时,所有的乘积的和为_________,当n=100时,所有的乘积的和为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
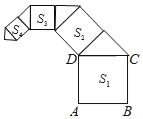
【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2018的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com