
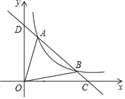
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЂйЃЌе§ЗНаЮABCDЃЌЕуEЁЂЕуFЗжБ№дкABКЭADЩЯЃЌЧвAE=AFЃЎДЫЪБЃЌЯпЖЮBEЁЂDFЕФЪ§СПЙиЯЕЪЧ ЃЌЮЛжУЙиЯЕЪЧ ЃЎЧыжБНгаДГіНсТлЃЎ
(2)ШчЭМЂк,ЕШбќжБНЧШ§НЧаЮFAEШЦжБНЧЖЅЕуAЫГЪБеыа§зЊЁЯІС,ЕБ0Ёу<ІС<90ЁуЪБ,СЌНгBEЁЂDF,ДЫЪБ(1)жаЕФНсТлЪЧЗёГЩСЂЃЌШчЙћГЩСЂЃЌЧыжЄУїЃЛШчЙћВЛГЩСЂЃЌЧыЫЕУїРэгЩЁЃ
(3)ШчЭМЂл,ЕШбќжБНЧШ§НЧаЮFAEШЦжБНЧЖЅЕуAЫГЪБеыа§зЊЁЯІС,ЕБ90Ёу<ІС<180ЁуЪБЃЌСЌНгBDЁЂDEЁЂEFЁЂFBЃЌЕУЕНЫФБпаЮBDEFЃЌдђЫГДЮСЌНгЫФБпаЮBDEFИїБпжаЕуЫљзщГЩЕФЫФБпаЮЪЧЪВУДЬиЪтЫФБпаЮ?ЧыжБНгаДГіНсТл.
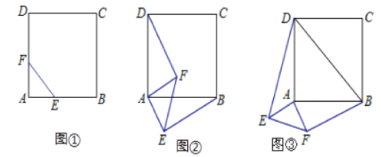
ЁОД№АИЁПЃЈ1ЃЉBE=DFЃЌBEЁЭDFЃЛЃЈ2ЃЉBE=DFЃЌBEЁЭDFЃЛжЄУїМћНтЮіЃЛЃЈ3ЃЉе§ЗНаЮ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОне§ЗНаЮЕФаджЪПЩЕУAB=ADЃЌЁЯA=90ЁуЃЌШЛКѓЧѓГіBE=DFЃЌBEЁЭDFЃЛ
ЃЈ2ЃЉИљОна§зЊНЧЧѓГіЁЯBAE=ЁЯDAFЃЌШЛКѓРћгУЁАБпНЧБпЁБжЄУїЁїABEКЭЁїADFШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУBE=DFЃЌШЋЕШШ§НЧаЮЖдгІНЧЯрЕШПЩЕУЁЯABE=ЁЯADFЃЌбгГЄDFНЛBEгкOЃЌЧѓГіЁЯABE+ЁЯ2=90ЁуЃЌДгЖјЕУЕНЁЯBOD=90ЁуЃЌИљОнДЙжБЕФЖЈвхЕУЕНBEЁЭDFЃЛ
ЃЈ3ЃЉСЌНгBEЁЂDFЃЌЭЌРэЧѓГіBE=DFЃЌBEЁЭDFЃЌдйИљОнЖдНЧЯпЯрЕШЧвЛЅЯрДЙжБЕФЫФБпаЮЕФжаЕузщГЩЕФЫФБпаЮЪЧе§ЗНаЮНтД№ЃЎ
(1)дке§ЗНаЮABCDжаЃЌAB=ADЃЌЁЯA=90ЁуЃЌ
ЁпAE=AFЃЌ
ЁрABAE=ADAFЃЌ
МДBE=DFЃЌ
ЁпЁЯA=90ЁуЃЌ
ЁрBEЁЭDFЃЌ
ЙЪBE=DFЃЌBEЁЭDFЃЛ
(2)ЁпЁїFAEЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAE=AFЃЌ
дке§ЗНаЮABCDжаЃЌAB=ADЃЌ
гжЁпЁЯBAE=ЁЯDAF=ІСЃЌ
ЁрдкЁїABEКЭЁїADFжаЃЌ
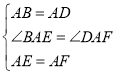 ЃЌ
ЃЌ
ЁрЁїABEЁеЁїADF(SAS)ЃЌ
ЁрBE=DFЃЌЁЯABE=ЁЯADFЃЌ
бгГЄDFНЛBEгкOЃЌ
ЁпЁЯADF+ЁЯ1=90ЁуЃЌЁЯ1=ЁЯ2(ЖдЖЅНЧЯрЕШ)ЃЌ
ЁрЁЯABE+ЁЯ2=90ЁуЃЌ
ЁрЁЯBOD=180Ёу90Ёу=90ЁуЃЌ
ЁрBEЁЭDFЃЌ
ЙЪBE=DFЃЌBEЁЭDFЃЛ
(3)СЌНгBEЁЂDFЃЌ
гы(2)ЭЌРэЧѓГіBE=DFЃЌBEЁЭDFЃЌ
ЙЪЫГДЮСЌНгЫФБпаЮBDEFИїБпжаЕуЫљзщГЩЕФЫФБпаЮЪЧе§ЗНаЮ.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
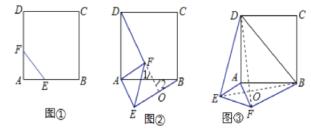
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкдВЁбOФкгаелЯпOABCЃЌЦфжаOA=8ЃЌAB=12ЃЌЁЯA=ЁЯB=60ЁуЃЌдђBCЕФГЄЮЊЃЈЁЁЁЁЃЉ
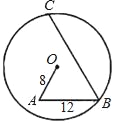
A. 19 B. 16 C. 18 D. 20
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃЭЈЙ§ГѕЦРОіЖЈзюКѓДгМзЁЂввЁЂБћШ§ИіАржаЭЦМівЛИіАрЮЊЯиМЖЯШНјАрМЏЬхЃЌЯТБэЪЧШ§ИіАрЕФЮхЯюЫижЪПМЦРЕУЗжБэЁЃ
ЮхЯюЫижЪПМЦРЕУЗжБэЃЈЕЅЮЛЃКЗжЃЉ
АрМЖ | ааЮЊЙцЗЖ | бЇЯАГЩМЈ | аЃдЫЖЏЛс | веЪѕЛёНБ | РЭЖЏЮРЩњ |
МзАр | 10 | 10 | 6 | 10 | 7 |
ввАр | 10 | 8 | 8 | 9 | 8 |
БћАр | 9 | 10 | 9 | 6 | 9 |
ИљОнЭГМЦБэжаЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыФуВЙШЋЮхЯюГЩМЈПМЦРЗжЮіБэжаЕФЪ§ОнЃК
АрМЖ | ЦНОљЗж | жкЪ§ | жаЮЛЪ§ |
МзАр | 8.6 | 10 | Ђл |
ввАр | 8.6 | Ђк | 8 |
БћАр | Ђй | 9 | 9 |
ЃЈ2ЃЉВЮееЩЯБэжаЕФЪ§ОнЃЌФуЭЦМіФФИіАрЮЊЯиМЖЯШНјАрМЏЬхЃПВЂЫЕУїРэгЩЁЃ
ЃЈ3ЃЉШчЙћбЇаЃАбааЮЊЙцЗЖЁЂбЇЯАГЩМЈЁЂаЃдЫЖЏЛсЁЂвеЪѕЛёНБЁЂРЭЖЏЮРЩњЮхЯюПМЦРГЩМЈАДее3ЁУ2ЁУ1ЁУ1ЁУ3ЕФБШШЗЖЈАрМЖЕФзлКЯГЩМЈЃЌбЇЩњДІЕФРюРЯЪІИљОнетИізлКЯГЩМЈЃЌЛцжЦСЫвЛЗљВЛЭъећЕФЬѕаЮЭГМЦЭМЃЌЧыНЋетИіЭГМЦЭМВЙГфЭъећЃЌАДееетИіГЩМЈЃЌгІЭЦМіФФИіАрЮЊЯиМЖЯШНјАрМЏЬхЃПЮЊЪВУДЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпy=kx+bгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓНЛгкAЃЈ1ЃЌmЃЉЁЂBСНЕуЃЌгыx жсЁЂyжсЗжБ№ЯрНЛгкCЃЈ4ЃЌ0ЃЉЁЂDСНЕуЃЎ
ЕФЭМЯѓНЛгкAЃЈ1ЃЌmЃЉЁЂBСНЕуЃЌгыx жсЁЂyжсЗжБ№ЯрНЛгкCЃЈ4ЃЌ0ЃЉЁЂDСНЕуЃЎ
ЃЈ1ЃЉЧѓжБЯпy=kx+bЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгOAЁЂOBЃЌЧѓЁїAOBЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГіЙигкxЕФВЛЕШЪНkx+bЃМ![]() ЕФНтМЏЪЧЁЁ ЁЁЃЎ
ЕФНтМЏЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
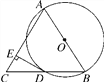
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌBDЪЧЁбOЕФЯвЃЌбгГЄBDЕНЕуCЃЌЪЙDCЃНBDЃЌСЌНгACЃЌЙ§ЕуDзїDEЁЭACЃЌДЙзуЮЊE.
(1)ЧѓжЄЃКABЃНACЃЛ
(2)ШєЁбOЕФАыОЖЮЊ4ЃЌЁЯBACЃН60ЁуЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌAЁЂBЗжБ№ЮЊЪ§жсЩЯЕФСНЕуЃЌAЕуЖдгІЕФЪ§ЮЊ-20ЃЌBЕуЖдгІЕФЪ§ЮЊ100ЃЎ
![]()
ЧыаДГіABжаЕуMЖдгІЕФЪ§ЁЃ
ЃЈ2ЃЉЯжгавЛжЛЕчзгТьвЯPДгBЕуГіЗЂЃЌвд6ЕЅЮЛ/УыЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБСэвЛжЛЕчзгТьвЯQЧЁКУДгAЕуГіЗЂЃЌвд4ЕЅЮЛ/УыЕФЫйЖШЯђгвдЫЖЏЁЃЩшСНжЛЕчзгТьвЯдкЪ§жсЩЯЕФCЕуЯргіЃЌФужЊЕРCЕуЖдгІЕФЪ§ЪЧЖрЩйТ№ЃП
ЃЈ3ЃЉШєЕБЕчзгТьвЯPДгBЕуГіЗЂЪБЃЌвд6ЕЅЮЛ/УыЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБСэвЛжЛЕчзгТьвЯQЧЁКУДгAЕуГіЗЂЃЌвд4ЕЅЮЛ/УыЕФЫйЖШвВЯђзѓдЫЖЏЁЃЩшСНжЛЕчзгТьвЯдкЪ§жсЩЯЕФDЕуЯргіЃЌФужЊЕРDЕуЖдгІЕФЪ§ЪЧЖрЩйТ№ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉЃЈ![]() x2y-2xy+y2ЃЉЃЈ-4xyЃЉЃЛ
x2y-2xy+y2ЃЉЃЈ-4xyЃЉЃЛ
ЃЈ2ЃЉ6mn2(2Ѓ![]() mn4)ЃЋ(Ѓ
mn4)ЃЋ(Ѓ![]() mn3)2ЃЛ
mn3)2ЃЛ
ЃЈ3ЃЉ-4x2ЁЄЃЈ![]() xy-y2ЃЉ-3xЁЄЃЈxy2-2x2yЃЉЃЛ
xy-y2ЃЉ-3xЁЄЃЈxy2-2x2yЃЉЃЛ
ЃЈ4ЃЉ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2+bxЉ![]() гыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉСНЕуЃЌЯжгаОЙ§ЕуAЕФжБЯпlЃКy=kx+b1гыyжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэИіНЛЕуЮЊDЃЎ
гыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉСНЕуЃЌЯжгаОЙ§ЕуAЕФжБЯпlЃКy=kx+b1гыyжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэИіНЛЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєЕуDдкЕкЖўЯѓЯоЧвТњзуCD=5ACЃЌЧѓДЫЪБжБЯп1ЕФНтЮіЪНЃЛдкДЫЬѕМўЯТЃЌЕуEЮЊжБЯп1ЯТЗНХзЮяЯпЩЯЕФвЛЕуЃЌЧѓЁїACEУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕуEЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЃЌЩшPдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвдкЕкЖўЯѓЯоЃЌЕНxжсЕФОрРыЮЊ4ЃЌЕуQдкХзЮяЯпЩЯЃЌШєвдЕуAЃЌDЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮФмЗёГЩЮЊЦНааЫФБпаЮЃПШєФмЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯA,ЁЯB,ЁЯCЕФЖдБпЗжБ№ЪЧa,b,cЃЌдђТњзуЯТСаЬѕМўЕЋВЛЪЧжБНЧШ§НЧаЮЕФЪЧЃЈ ЃЉ
A.a2Ѓc2=b2B.a=n2Ѓ1, b=2n, c=n2ЃЋ1 ( nЃО1ЃЉ
C.ЁЯAЃКЁЯBЃКЁЯC = 3ЃК4ЃК5D.ЁЯAЃНЁЯB =![]() ЁЯC
ЁЯC
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com