
【题目】学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为县级先进班集体,下表是三个班的五项素质考评得分表。
五项素质考评得分表(单位:分)
班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
甲班 | 10 | 10 | 6 | 10 | 7 |
乙班 | 10 | 8 | 8 | 9 | 8 |
丙班 | 9 | 10 | 9 | 6 | 9 |
根据统计表中的信息回答下列问题:
(1)请你补全五项成绩考评分析表中的数据:
班级 | 平均分 | 众数 | 中位数 |
甲班 | 8.6 | 10 | ③ |
乙班 | 8.6 | ② | 8 |
丙班 | ① | 9 | 9 |
(2)参照上表中的数据,你推荐哪个班为县级先进班集体?并说明理由。
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3∶2∶1∶1∶3的比确定班级的综合成绩,学生处的李老师根据这个综合成绩,绘制了一幅不完整的条形统计图,请将这个统计图补充完整,按照这个成绩,应推荐哪个班为县级先进班集体?为什么?

【答案】(1)8.6,8,10;(2)甲班:三个班的平均数相同,甲班众数与中位数高于乙和丙;(3)画图见解析,丙班.
【解析】
(1)根据平均数是所有数据的和除以数据的个数,众数是出现次数最多的数据,中位数是一组数据按从小到大或从大到小的顺序排列中间的数(或中间两个数的平均数),可得答案;
(2)根据平均数、众数、中位数的大小比较,可得答案;
(3)根据加权平均数的大小比较,可得答案.
(1) ①![]() =(9+10+9+6+9)
=(9+10+9+6+9)![]() =8.6,②观察五项素质考评得分表可知乙班的众数是8,③观察五项素质考评得分表可知甲班的中位数是10;
=8.6,②观察五项素质考评得分表可知乙班的众数是8,③观察五项素质考评得分表可知甲班的中位数是10;
(2)甲班,理由为:三个班的平均数相同,甲班的众数与中位数都高于乙班与丙班;
(3)根据题意,得:丙班的平均数为9×![]() +10×
+10×![]() +9×
+9×![]() +6×
+6×![]() +9×
+9×![]() =8.9
=8.9
补全条形统计图,如图所示
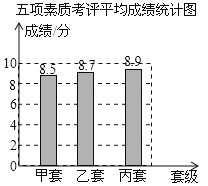
∵8.5<8.7<8.9,
∴依照这个成绩,应推荐丙班为市级先进班集体.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】数轴上两点之间的距离等于相应两数差的绝对值,即:点A、B表示的数分别为a、b,这两点之间的距离为AB=![]() ,如:表示数1与5的两点之间的距离可表示为
,如:表示数1与5的两点之间的距离可表示为![]() ,表示数-2与3的两点之间的距离可表示为
,表示数-2与3的两点之间的距离可表示为![]() .
.
(1)数轴上表示2和7的两点之间的距离是 ,数轴上表示3和-6的两点之间的距离是 ;
(2)数轴上表示x和-2的两点M和N之间的距离是 ,如果![]() ,则x为 ;
,则x为 ;
(3)当式子:![]() 取最小值时,x的值为 ,最小值为 .
取最小值时,x的值为 ,最小值为 .
(借助数轴,画出图形,写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.

(1)根据图象,求当x≥3时的函数关系式;
(2)某人乘坐2.5km,应付多少钱?
(3)某人乘坐13km,应付多少钱?
(4)若某人付车费30.8元,出租车行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 观察下列三行数:
2,4,8,16,32,![]()
![]() ,1,2,4,8,
,1,2,4,8,![]()
1,5,7,17,31,![]()
如图,第一行数的第n(n为正整数)个数![]() 用来表示,第二行数的第n个数用
用来表示,第二行数的第n个数用![]() 来表示,第三行数的第n个数用
来表示,第三行数的第n个数用![]() 来表示
来表示
(1)根据你发现的规律,请用含n的代数式表示数![]() ,
,![]() ,
,![]() 的值
的值![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ;
(2)取每行的第6个数,计算这三个数的和
(3)若![]() 记为x,求
记为x,求![]() (结果用含x的式子表示并化简)
(结果用含x的式子表示并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)。
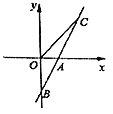
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△AOC =2,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a1=22-02,a2=32-12,…,an=(n+1)2-(n-1)2(n为大于1的整数)
(1)计算a15的值;
(2)通过拼图你发现前三个图形的面积之和与第四个正方形的面积之间有什么关系:
__________________________________(用含a、b的式子表示);

(3)根据(2)中结论,探究an=(n+1)2-(n-1)2是否为4的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
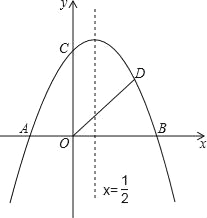
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=
x2+bx+c与x轴交于A、B两点(A在B点左侧),与y轴交于点C,对称轴为直线x=![]() ,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);
,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限);
(1)求抛物线的解析式和点D的坐标;
(2)点M是抛物线上的动点,在x轴上存在一点N,使得A、D、M、N四个点为顶点的四边形是平行四边形,求出点M的坐标;
(3)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
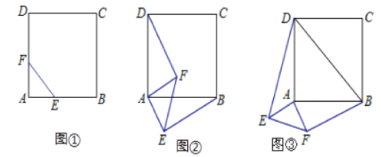
【题目】(1)如图①,正方形ABCD,点E、点F分别在AB和AD上,且AE=AF.此时,线段BE、DF的数量关系是 ,位置关系是 .请直接写出结论.
(2)如图②,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由。
(3)如图③,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB,得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点A(2,0),B(0,4).
(1)求此函数的解析式;
(2)若点P为此一次函数图象上一动点,且△POA的面积为2,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com