
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2+bxЉ![]() гыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉСНЕуЃЌЯжгаОЙ§ЕуAЕФжБЯпlЃКy=kx+b1гыyжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэИіНЛЕуЮЊDЃЎ
гыxжсНЛгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉСНЕуЃЌЯжгаОЙ§ЕуAЕФжБЯпlЃКy=kx+b1гыyжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэИіНЛЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєЕуDдкЕкЖўЯѓЯоЧвТњзуCD=5ACЃЌЧѓДЫЪБжБЯп1ЕФНтЮіЪНЃЛдкДЫЬѕМўЯТЃЌЕуEЮЊжБЯп1ЯТЗНХзЮяЯпЩЯЕФвЛЕуЃЌЧѓЁїACEУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕуEЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЃЌЩшPдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвдкЕкЖўЯѓЯоЃЌЕНxжсЕФОрРыЮЊ4ЃЌЕуQдкХзЮяЯпЩЯЃЌШєвдЕуAЃЌDЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮФмЗёГЩЮЊЦНааЫФБпаЮЃПШєФмЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ЙлВьЯТСаШ§ааЪ§:
2,4,8,16,32,![]()
![]() ,1,2,4,8,
,1,2,4,8,![]()
1,5,7,17,31,![]()
ШчЭМ,ЕквЛааЪ§ЕФЕкn(nЮЊе§ећЪ§)ИіЪ§![]() гУРДБэЪО,ЕкЖўааЪ§ЕФЕкnИіЪ§гУ
гУРДБэЪО,ЕкЖўааЪ§ЕФЕкnИіЪ§гУ![]() РДБэЪО,ЕкШ§ааЪ§ЕФЕкnИіЪ§гУ
РДБэЪО,ЕкШ§ааЪ§ЕФЕкnИіЪ§гУ![]() РДБэЪО
РДБэЪО
ЃЈ1ЃЉИљОнФуЗЂЯжЕФЙцТЩ,ЧыгУКЌnЕФДњЪ§ЪНБэЪОЪ§![]() ,
,![]() ,
,![]() ЕФжЕ
ЕФжЕ![]() = ЃЛ
= ЃЛ ![]() = ЃЛ
= ЃЛ ![]() = ЃЛ
= ЃЛ
ЃЈ2ЃЉШЁУПааЕФЕк6ИіЪ§,МЦЫуетШ§ИіЪ§ЕФКЭ
ЃЈ3ЃЉШє![]() МЧЮЊx,Чѓ
МЧЮЊx,Чѓ![]() (НсЙћгУКЌxЕФЪНзгБэЪОВЂЛЏМђ)
(НсЙћгУКЌxЕФЪНзгБэЪОВЂЛЏМђ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
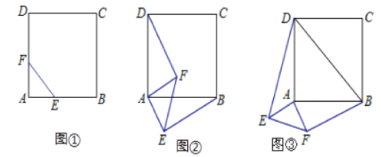
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЂйЃЌе§ЗНаЮABCDЃЌЕуEЁЂЕуFЗжБ№дкABКЭADЩЯЃЌЧвAE=AFЃЎДЫЪБЃЌЯпЖЮBEЁЂDFЕФЪ§СПЙиЯЕЪЧ ЃЌЮЛжУЙиЯЕЪЧ ЃЎЧыжБНгаДГіНсТлЃЎ
(2)ШчЭМЂк,ЕШбќжБНЧШ§НЧаЮFAEШЦжБНЧЖЅЕуAЫГЪБеыа§зЊЁЯІС,ЕБ0Ёу<ІС<90ЁуЪБ,СЌНгBEЁЂDF,ДЫЪБ(1)жаЕФНсТлЪЧЗёГЩСЂЃЌШчЙћГЩСЂЃЌЧыжЄУїЃЛШчЙћВЛГЩСЂЃЌЧыЫЕУїРэгЩЁЃ
(3)ШчЭМЂл,ЕШбќжБНЧШ§НЧаЮFAEШЦжБНЧЖЅЕуAЫГЪБеыа§зЊЁЯІС,ЕБ90Ёу<ІС<180ЁуЪБЃЌСЌНгBDЁЂDEЁЂEFЁЂFBЃЌЕУЕНЫФБпаЮBDEFЃЌдђЫГДЮСЌНгЫФБпаЮBDEFИїБпжаЕуЫљзщГЩЕФЫФБпаЮЪЧЪВУДЬиЪтЫФБпаЮ?ЧыжБНгаДГіНсТл.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮжНЦЌABCDжаЃЌABЃН4ЃЌBCЃН8ЃЌНЋжНЦЌбиEFелЕўЃЌЪЙЕуCгыЕуAжиКЯЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈ ЃЉ

A. AFЃНAE B. ЁїABEЁеЁїAGF C. EFЃН![]() D. AFЃНEF
D. AFЃНEF
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгквЛИіДѓгк1ЕФе§ећЪ§nНјааШчЯТВйзїЃК
Ђй НЋnВ№ЗжЮЊСНИіе§ећЪ§aЁЂbЕФКЭЃЌВЂМЦЫуГЫЛ§aЁСb
Ђк Ждгке§ећЪ§aЁЂbЗжБ№жиИДДЫВйзїЃЌЕУЕНСэЭтСНИіГЫЛ§
Ђл жиИДЩЯЪіЙ§ГЬЃЌжБжСВЛФмдйВ№ЗжЮЊжЙЃЈМДВ№ЗжЕНе§ећЪ§1ЃЉ
ЕБnЃН6ЪБЃЌЫљгаЕФГЫЛ§ЕФКЭЮЊ_________ЃЌЕБnЃН100ЪБЃЌЫљгаЕФГЫЛ§ЕФКЭЮЊ_________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХШЫУЧЛЗБЃвтЪЖЕФдіЧПЃЌЁАЕЭЬМГіааЁБдНРДдНЮЊШЫУЧЫљГЋЕМЁЃаЁРювЊДгМвЯчЕНФўВЈЙЄзїЃЌШєГЫЗЩЛњашвЊ3аЁЪБЃЌГЫЦћГЕашвЊ9аЁЪБЁЃетСНжжНЛЭЈЙЄОпУПаЁЪБХХЗХЕФЖўбѕЛЏЬМзмСПЮЊ80ЧЇПЫЃЌвбжЊЗЩЛњУПаЁЪБЖўбѕЛЏЬМЕФХХЗХСПБШЦћГЕЖр46ЧЇПЫЃЌШєаЁРюГЫЦћГЕРДФўВЈЃЌФЧУДЫћДЫаагыГЫЗЩЛњЯрБШНЋМѕЩйЖўбѕЛЏЬМХХЗХСПЖрЩйЧЇПЫ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§ЕФЭМЯѓОЙ§ЕуA(2,0),B(0,4).
ЃЈ1ЃЉЧѓДЫКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPЮЊДЫвЛДЮКЏЪ§ЭМЯѓЩЯвЛЖЏЕуЃЌЧвЁїPOAЕФУцЛ§ЮЊ2ЃЌЧѓЕуPЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊAЁЂBЁЂCШ§ЕудкЪ§жсЩЯЕФЮЛжУШчЭМЫљЪОЃЌЫќУЧБэЪОЕФЪ§ЗжБ№ЪЧaЁЂbЁЂc

(1) ЬюПеЃКabc________0ЃЌaЃЋb________acЃЌabЃac________0ЃЛЃЈЬюЁАЃОЁБЃЌЁАЃНЁБЛђЁАЃМЁБЃЉ
(2) Шє|a|ЃН2ЃЌЧвЕуBЕНЕуAЁЂCЕФОрРыЯрЕШ
Ђй ЕБb2ЃН16ЪБЃЌЧѓcЕФжЕ
Ђк ЧѓbЁЂcжЎМфЕФЪ§СПЙиЯЕ
Ђл PЪЧЪ§жсЩЯBЃЌCСНЕужЎМфЕФвЛИіЖЏЕуЩшЕуPБэЪОЕФЪ§ЮЊxЃЎЕБPЕудкдЫЖЏЙ§ГЬжаЃЌbxЃЋcxЃЋ|xЃc|Ѓ10|xЃЋa|ЕФжЕБЃГжВЛБфЃЌЧѓbЕФжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌЖдГЦжсЮЊx=![]() ЃЌЧвОЙ§ЕуЃЈ2ЃЌ0ЃЉЃЌгаЯТСаЫЕЗЈЃКЂйabcЃМ0ЃЛЂкa+b=0ЃЛЂлaЉb+c=0ЃЛЂмШєЃЈ0ЃЌy1ЃЉЃЌЃЈ1ЃЌy2ЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌдђy1=y2ЃЎЩЯЪіЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
ЃЌЧвОЙ§ЕуЃЈ2ЃЌ0ЃЉЃЌгаЯТСаЫЕЗЈЃКЂйabcЃМ0ЃЛЂкa+b=0ЃЛЂлaЉb+c=0ЃЛЂмШєЃЈ0ЃЌy1ЃЉЃЌЃЈ1ЃЌy2ЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌдђy1=y2ЃЎЩЯЪіЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ

AЃЎЂйЂкЂлЂм BЃЎЂлЂм CЃЎЂйЂлЂм DЃЎЂйЂк
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com