
分析 (1)设A型和B型洗衣机每台的销售利润各是a元和b元,根据销售15台A型和10台B型洗衣机可获得利润为6000元,销售10台A型和15台B型洗衣机的利润6500元,即可列方程组求得a和b的值;
(2)①根据两种型号的利润的和就是总利润即可列出函数解析式;
②根据一次函数的性质,即可求解.
解答 解:(1)设A型和B型洗衣机每台的销售利润各是a元和b元.
则$\left\{\begin{array}{l}{15a+10b=6000}\\{10a+15b=6500}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=200}\\{b=300}\end{array}\right.$.
答:A型和B型洗衣机每台的销售利润各是200元和300元;
(2)①根据题意得y=200x+300(160-x),即y=-100x+48000;
②根据题意得:160-x≤2x,解得:x≥53$\frac{1}{3}$,
∵y=-100x+48000中,k=-100<0,
∴y随x的增大而减小.
∵x为正整数,
∴当x=54时,y取得最大值,此时160-x=106.
答:该商店购进A型、B型洗衣机各54台和106台时,才能使销售利润最大.
点评 本题考查了二元一次方程组以及一次函数的应用,求最值需先求函数表达式,再运用函数性质求解.此题的关键在列式表示利润和台数之间的函数关系式.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
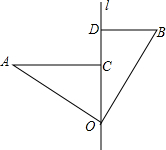 如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.已知AC=6,BD=4,则CD=2.
如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.已知AC=6,BD=4,则CD=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
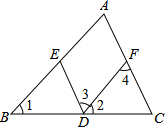 如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.
如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com