
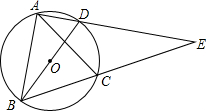
 如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.分析 (1)结合已知条件就可以推出∠ABC=∠ADB,再加上公共角就可以推出结论;
(2)由(1)的结论就可以推出AB长度,规矩勾股定理即可推出⊙O半径的长.
解答 (1)证明:∵AB=AC,
∴$\widehat{AB}=\widehat{AC}$,
∴∠ABC=∠ADB,
又∠BAE=∠DAB,
∴△ABD∽△AEB;
(2)解:∵△ABD∽△AEB,
∴$\frac{AB}{AE}=\frac{AD}{AB}$,
∵AD=1,DE=3,
∴AE=4,
∴AB2=AD•AE=1×4=4,
∴AB=2,
∵BD是⊙O的直径,
∴∠DAB=90°,
在Rt△ABD中,BD2=AB2+AD2=22+12=5,
∴BD=$\sqrt{5}$,
∴⊙O半径的长是$\frac{\sqrt{5}}{2}$.
点评 本题主要考查了勾股定理、相似三角形的判定和性质、圆周角定理,解题的关键在于找到∠ABC=∠ADB,求证三角形相似.


科目:初中数学 来源: 题型:解答题
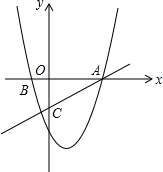 如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$.
如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{{a^2}+a}}{a}$ | B. | $\frac{a}{{{a^2}+1}}$ | C. | $\frac{a}{{{a^2}-1}}$ | D. | $\frac{1}{{{a^2}-1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
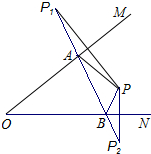 如图,∠MON内有一点P,PP1、PP2分别被OM、ON垂直平分,P1P2与OM、ON分别交于点A、B.若P1P2=10cm,则△PAB的周长为10cm.
如图,∠MON内有一点P,PP1、PP2分别被OM、ON垂直平分,P1P2与OM、ON分别交于点A、B.若P1P2=10cm,则△PAB的周长为10cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com