
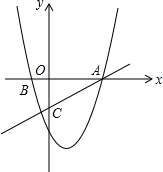
 如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$.
如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$. 分析 根据抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,可以画出相应的图形,进而可以得到点P的坐标;要求点Q的纵坐标取值范围,关键是能够根据题目中给出的信息,构造出相应的角,通过题目中的额已有信息,灵活变化,从而可以解答本题.
解答 解:将x=0代入y=$\frac{1}{3}$x-1得,y=-1;将y=0代入y=$\frac{1}{3}$x-1得,x=3.
∵直线y=$\frac{1}{3}$x-1交y轴于点C,交x轴于点A,
∴点A的坐标为(3,0),点C的坐标为(0,-1).
∵x轴上的点P满足PA=PC,设点P的坐标为(x,0),如下图一所示: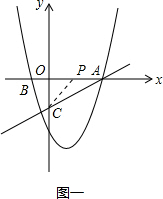
∴3-x=$\sqrt{{x}^{2}+(-1)^{2}}$.
解得,x=$\frac{4}{3}$.
故点P的坐标为($\frac{4}{3},0$).
如下图二所示,作CD=PD,点D在x轴上,设DP的长度为a,CD的延长线交抛物线的对称轴于点Q2,CP交抛物线的对称轴于点Q1,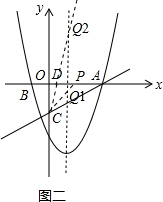
∵抛物线y=x2-2x-3.
∴抛物线的对称轴为:x=$-\frac{-2}{2×1}=1$.
∵点Q1,Q2位于抛物线的对称轴上,设点Q1,Q2的坐标分别为(1,y1),(1,y2),
又∵PC=PA,
∴∠OAC=∠Q1CA.
∵点C的坐标为(0,-1),点P的坐标为:($\frac{4}{3},0$),设过点CP的直线为:y=kx+b.
∴$\left\{\begin{array}{l}{b=-1}\\{\frac{4}{3}k+b=0}\end{array}\right.$
解得,k=$\frac{3}{4}$,b=-1.
∴y=$\frac{3}{4}x-1$.
将x=1代入y=$\frac{3}{4}x-1$得,y=$-\frac{1}{4}$.
故点Q1的坐标为(1,-$\frac{1}{4}$).
∵CD=PD,PC=PA,∠DPC=∠OAC+∠PCA,
∴∠OAC=∠PCA,∠DPC=∠DCP,∠DCP=2∠OAC.
∴∠Q2CA=3∠OAC.
∵DP的长度为a,点P的坐标为($\frac{4}{3},0$),
∴点D的坐标为($\frac{4}{3}-a,0$).
∴$\sqrt{(-1)^{2}+(\frac{4}{3}-a)^{2}}={a}^{2}$.
解得,a=$\frac{25}{24}$.
∴点D的坐标为($\frac{7}{24},0$).
设过点D($\frac{7}{24},0$)、C(0,-1)的直线解析式为y=mx+n.
$\left\{\begin{array}{l}{\frac{7}{24}m+n=0}\\{n=-1}\end{array}\right.$
解得,m=$\frac{24}{7}$,n=-1.
∴y=$\frac{24}{7}x-1$.
将x=1代入y=$\frac{24}{7}x-1$得,y=$\frac{17}{7}$.
故Q2的坐标为(1,$\frac{17}{7}$).
∵在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,
∴点Q纵坐标y取值范围为:0<y<$\frac{17}{7}$.
故答案为:($\frac{4}{3},0$),0<y<$\frac{17}{7}$.
点评 本题考查抛物线与x轴的交点问题、直线与二次函数相交的问题,解答本题的关键是可以根据题意画出相应的图形,构造出题目中的角,灵活变化求出所求问题的答案.


科目:初中数学 来源: 题型:选择题

| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2013\sqrt{3}}{2014}$ | D. | $\frac{2014\sqrt{3}}{2015}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
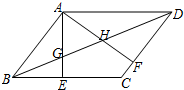 如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于GH.
如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于GH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
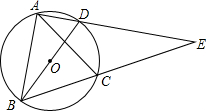 如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com