
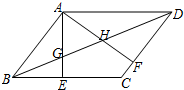
 如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于GH.
如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于GH.分析 (1)利用两角对应相等可证出△ABE∽△ADF;
(2)利用(1)的结论,先证出△ABG≌△ADH,得到AB=AD,那么平行四边形ABCD是菱形.
解答 解:(1)∵AE⊥BC于E,AF⊥CD于F,
∴∠AEB=∠AFD=90°,
∵四边形ABCD是平行四边形,
∴∠ABE=∠ADF,
∴△ABE∽△ADF;
(2)证明:∵AG=AH,
∴∠AGH=∠AHG,
∴∠AGB=∠AHD,
∵△ABE∽△ADF,
∴∠BAG=∠DAH,
在△BAG与△DAH中,$\left\{\begin{array}{l}{∠AGB=∠AHD}\\{∠BAG=∠DAH}\\{AG=AH}\end{array}\right.$,
∴△BAG≌△DAH,
∴AB=AD,
∵四边形ABCD是平行四边形,
AB=AD,
∴平行四边形ABCD是菱形.
点评 本题考查了相似三角形的判定与性质、平行四边形的性质、菱形的判定,熟悉图形特征是解题的关键.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
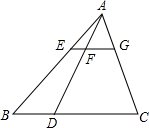 如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.
如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
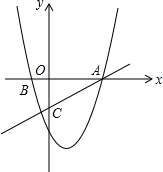 如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$.
如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
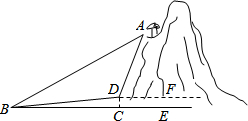 我市AAAA景区有一处景观奇异的望天洞,D点是望天洞的入口,游人从入口进洞后,可经山洞到山顶的出口亭A处观光,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD的长为120米,坡角为∠DBC=10°,在B出测得A的仰角∠ABC=40°,在D出测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.
我市AAAA景区有一处景观奇异的望天洞,D点是望天洞的入口,游人从入口进洞后,可经山洞到山顶的出口亭A处观光,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD的长为120米,坡角为∠DBC=10°,在B出测得A的仰角∠ABC=40°,在D出测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任何数与0相乘都得0 | B. | 0是最小的有理数 | ||
| C. | 绝对值最小的有理数是0 | D. | 0没有倒数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
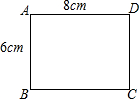 在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com