
分析 (1)先算括号里面的,再算除法即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)原式=$\frac{-(x-y)}{xy}$•$\frac{xy}{(x+y)(x-y)}$
=-$\frac{1}{x+y}$;
(2)$\left\{\begin{array}{l}3(x-1)≤4x①\\ 3-\frac{3}{2}x≥\frac{1}{2}x+1②\end{array}\right.$,
解不等式①,得x>-3,
解不等式②,得x≤1,
所以原不等式组的解集为-3<x≤1.
点评 本题考查的是分式的混合运算,分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
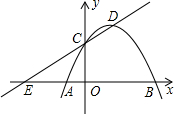 如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.
如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
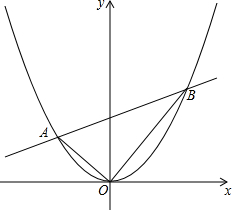 已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)
已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com