
【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 | 视力 | 频数(人) |
|
| 20 |
|
|
|
|
|
|
|
| 70 |
|
| 10 |
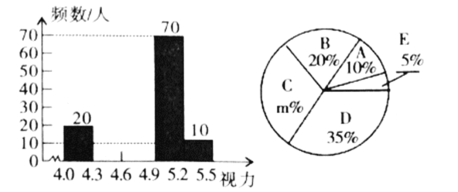
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)![]() ___________,
___________,![]() _____________,
_____________,![]() _____________;
_____________;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?
【答案】(1)200;(2)40,60,30;(3)见详解;(4)视力正常的人数占被统计人数的百分比是40%
【解析】
(1)先根据4.0x<4.3的频数除以频率求出被调查的总人数,
(2)用总人数乘以频率20%计算即可得到a,用总人数减去其他频数求出b,再用b除以总人数,即可求出m的值;
(3)根据(2)求出的a,b的值,即可补全统计图;
(4)求出后两组的频率之和即可求出视力正常的人数占被统计人数的百分比,即可得解.
解:(1)抽样调查的人数是:![]() 人;
人;
(2)a=200×20%=40,b=200(20+40+70+10)=60,m%=60÷200×100%=30%,即m=30,
故答案为40,60,30;
(3)根据(2)求出的![]() 的值,补图如下:
的值,补图如下:
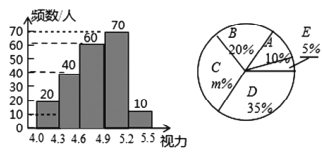
(4)35%+5%=40%,
答:视力正常的人数占被统计人数的百分比是40%.


科目:初中数学 来源: 题型:
【题目】如图,从左至右第1个图由1个正六边形,6个正方形和6个等边三角形组成;第二个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成按此规律,第![]() 个图中正方形和等边三角形的个数之和为( )
个图中正方形和等边三角形的个数之和为( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的一块地(图中阴影部分),∠ADC=90°,AD=12,CD=9,AB=25,BC=20.
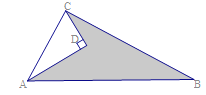
(1)求∠ACB的度数;
(2)求阴影部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①△ABF≌△ADF;②S△ADF=2S△CEF;③tan∠EBF=![]() ;④S△ABF=4S△BEF,其中正确结论的个数是( )
;④S△ABF=4S△BEF,其中正确结论的个数是( )
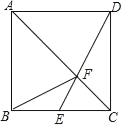
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
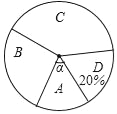
【题目】我市某中学举行演讲比赛,赛后整理参赛学生的成绩,将比赛成绩分为A,B,C,D四个等级,把结果列成下表(其中,m是常数)并绘制如图所示的扇形统计图(部分).
等级 | A | B | C | D |
人数 | 6 | 10 | m | 8 |
(1)求m的值和A等级所占圆心角α的大小;
(2)若从本次比赛中获得A等级的学生中,选出2名取参加市中心学生演讲比赛,已知A等级中男生有2名,求出所选2名学生中恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了甲、乙两种型号的中性笔共4000支,甲型号中性笔进价是3元/支,乙型号中性笔进价是7元/支,购进两种型号的中性笔共用去16000元.
(1)求甲、乙两种型号的中性笔各购进了多少支;
(2)为使每支乙型号中性笔的利润是甲型号的1.8倍,且保证售完这4000支中性笔的利润不低于7200元,求每支甲型号中性笔的售价至少是多少元.(注:利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确( )
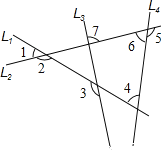
A. ∠2=∠4+∠7 B. ∠3=∠1+∠6 C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同的棱长为![]() 的小正方体堆成一个几何体,如下图所示.
的小正方体堆成一个几何体,如下图所示.
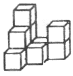



(1)该几何体是由 个小正方体组成,请画出它的主视图、左视图、俯视图(网格中所画的图形要画出各个正方形边框并涂上阴影).
(2)如果在这个几何体露在外面的表面喷上黄色的漆,每平方厘米用2克,则共需 克漆.
(3)这个几何体上,再添加一些相同的小正方体并保持这个几何体的俯视图和左视图不变,那么最多可以再添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】首先,我们学习一道“最值”问题的解答:
问题:已知x>0,求![]() 的最小值.
的最小值.
解答:对于x>0,我们有: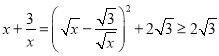
当![]() ,即
,即![]() 时,上述不等式取等号,所以
时,上述不等式取等号,所以![]() 的最小值是
的最小值是![]()
由解答知,![]() 的最小值是
的最小值是![]() .
.
弄清上述问题及解答方法之后,解答下述问题:
(1)求![]() 的最小值.
的最小值.
(2)在直角坐标系 xOy 中,一次函数![]() 的图象与 x 轴、 y 轴分别交于 A 、 B 两点.
的图象与 x 轴、 y 轴分别交于 A 、 B 两点.
①求 A 、 B 两点的坐标;
②求当OAB 的面积值等于![]() 时,用b 表示 k ;
时,用b 表示 k ;
③在②的条件下,求AOB 面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com