
【题目】我市某中学举行演讲比赛,赛后整理参赛学生的成绩,将比赛成绩分为A,B,C,D四个等级,把结果列成下表(其中,m是常数)并绘制如图所示的扇形统计图(部分).
等级 | A | B | C | D |
人数 | 6 | 10 | m | 8 |
(1)求m的值和A等级所占圆心角α的大小;
(2)若从本次比赛中获得A等级的学生中,选出2名取参加市中心学生演讲比赛,已知A等级中男生有2名,求出所选2名学生中恰好是一名男生和一名女生的概率.
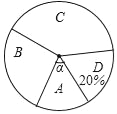
【答案】(1)m=16,A等级所占圆心角α=54°;(2)所选2名学生中恰好是一名男生和一名女生的概率为![]() .
.
【解析】分析:(1)先根据D等级人数及其百分比求得被调查的总人数,再用总人数减去A、B、D的人数求得m的值,用360°乘以A等级人数所占比例即可求出α的大小.
(2)设两位男生为a、b,四位女生为m、n、p、q,列出所有等可能结果,利用概率公式计算可得.
详解:(1)本次调查的总人数为8÷20%=40人,
则m=40﹣(6+10+8)=16,A等级所占圆心角α=360°×![]() =54°;
=54°;
(2)设两位男生为a、b,四位女生为m、n、p、q,
从6位同学中选取两人的所有等可能结果为:ab、am、an、ap、aq、bm、bn、bp、bq、mn、mp、mq、np、nq、pq共15种情况,
其中恰有1男1女的有8种结果,
所以所选2名学生中恰好是一名男生和一名女生的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】点O在直线PQ上,过点O作射线OC,使∠POC=130°,将一直角三角板的直角顶点放在点O处.
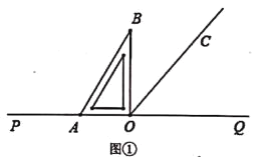
(1)如图①所示,将直角三角板AOB的一边OA与射线OP重合,则∠BOC=________°.
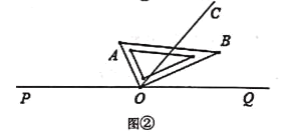
(2)将图①中的直角三角板AOB绕点O旋转一定角度得到如图②所示的位置,若OA平分∠POC,求∠BOQ的度数.
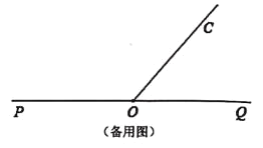
(3)将图①中的直角三角板AOB绕点O旋转一周,存在某一时刻恰有OB⊥OC,求出所有满足条件的∠AOQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0) ,与过A点的直线相交于另一点D(3,![]() ) ,过点D作DC⊥x轴,垂足为C.
) ,过点D作DC⊥x轴,垂足为C.
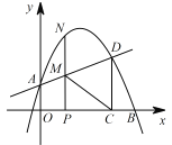
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O,C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM 面积的最大值;
(3)若P 是x 轴正半轴上的一动点,设OP 的长为t.是否存在t,使以点M,C,D,N 为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程(x+1)(x﹣2)=10根的情况是( )
A. 无实数根 B. 有两个正根
C. 有两个根,且都大于﹣1 D. 有两个根,其中一根大于2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个盛水的圆柱体玻璃容器,它的底面半径为![]() (容器厚度忽略不计),容器内水的高度为
(容器厚度忽略不计),容器内水的高度为![]() .
.
(1)如图1, 容器内水的体积为_ ![]() (结果保留
(结果保留![]() ).
).
(2)如图2,把一根半径为![]() ,高为
,高为![]() 的实心玻璃棒插入水中(玻璃棒完全淹没于水中),求水面上升的高度是多少?
的实心玻璃棒插入水中(玻璃棒完全淹没于水中),求水面上升的高度是多少?
(3)如图3,若把一根半径为![]() ,足够长的实心玻璃棒插入水中,求水面上升的高度是多少?
,足够长的实心玻璃棒插入水中,求水面上升的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 | 视力 | 频数(人) |
|
| 20 |
|
|
|
|
|
|
|
| 70 |
|
| 10 |
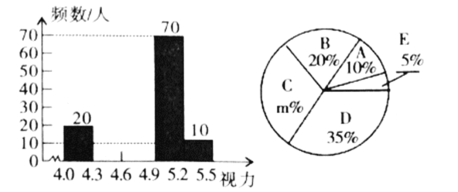
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)![]() ___________,
___________,![]() _____________,
_____________,![]() _____________;
_____________;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。
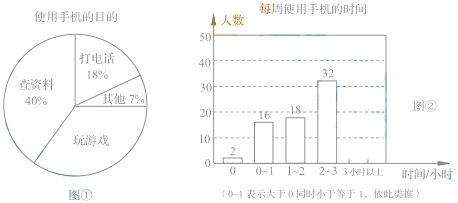
请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
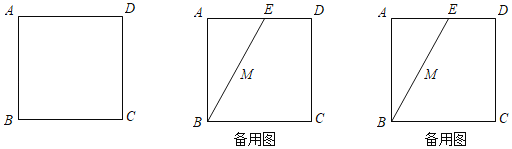
【题目】如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
(1)利用尺规作图(保留作图痕迹):分别以点B、C为圆心,BC长为半径作弧交正方形内部于点T,连接BT并延长交边AD于点E,则∠AEB=60°;
(2)在前面的条件下,取BE中点M,过点M的直线分别交边AB、CD于点P、Q.
①当PQ⊥BE时,求证:BP=2AP;
②当PQ=BE时,延长BE,CD交于N点,猜想NQ与MQ的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM ,DC的延长线相交于点E,则AB的长为_____________;
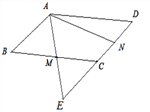
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com