
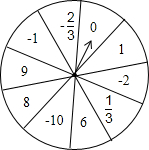
 如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?
如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?分析 (1)用正数的个数除以总个数即可得;
(2)用正整数的个数除以总个数即可得;
(3)用绝对值小于6的数的个数除以总个数可得;
(4)用绝对值大于8的数的个数除以总个数可得.
解答 解:(1)∵转盘中10个数,正数有1、$\frac{1}{3}$、6、8、9这5个,
∴P(转得正数)=$\frac{5}{10}$=$\frac{1}{2}$;
(2)∵转盘中10个数,正整数有1、6、8、9这4个,
∴P(转得正整数)=$\frac{4}{10}$=$\frac{2}{5}$;
(3)∵转盘中10个数,绝对值小于6的有0、1、-2、$\frac{1}{3}$、-1、-$\frac{2}{3}$这6个,
∴P(转得绝对值小于6)=$\frac{6}{10}$=$\frac{3}{5}$;
(4)∵转盘中10个数,绝对值大于8的有-10、9这2个,
∴P(转得绝对值大于8)=$\frac{2}{10}$=$\frac{1}{5}$.
点评 本题考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
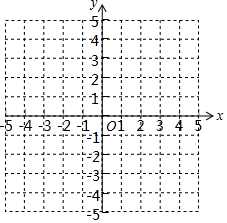 已知A(-3,-2),B(2,-2),C(3,1),D(-2,1)四个点.
已知A(-3,-2),B(2,-2),C(3,1),D(-2,1)四个点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
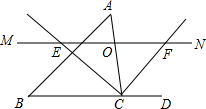 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.
如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
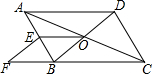 如图,在?ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD
如图,在?ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com