
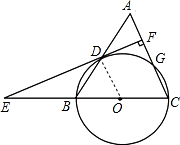
 如图所示,△ABC中,AC=BC,以BC为直径作⊙O交AB于点D,交AC于点G,作直线DF⊥AC交AC于点F,交CB的延长线于点E.
如图所示,△ABC中,AC=BC,以BC为直径作⊙O交AB于点D,交AC于点G,作直线DF⊥AC交AC于点F,交CB的延长线于点E.| 3 |
| 1 |
| 2 |
| 3 |
| 6 |
| 2 |
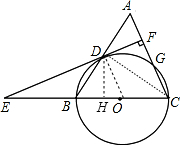 (2)解:连结CD,作DH⊥BC于H,如图,
(2)解:连结CD,作DH⊥BC于H,如图,| 1 |
| 2 |
| 3 |
| BC2-BD2 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||||
| 6 |
| 2 |
| OD2-DH2 |
| DH |
| DE |
| OH |
| OD |
2
| ||
| DE |
| 1 |
| 3 |
| 2 |


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
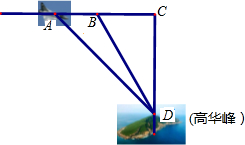 钓鱼岛自古以来就是我国神圣领土,2012年9月21日,国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并开始对钓鱼岛进行常态化立体巡航.如图,再一次巡航过程中,混巡航飞机飞行高度为4148米,在点A测得高华峰顶D点俯角为45°,飞机保持方向不变,前进1600米到达B点后测得D点俯角为60°,请据此钓鱼岛的最高峰海拔高度DE约为多少米.(结果保留整数,参考数值:
钓鱼岛自古以来就是我国神圣领土,2012年9月21日,国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并开始对钓鱼岛进行常态化立体巡航.如图,再一次巡航过程中,混巡航飞机飞行高度为4148米,在点A测得高华峰顶D点俯角为45°,飞机保持方向不变,前进1600米到达B点后测得D点俯角为60°,请据此钓鱼岛的最高峰海拔高度DE约为多少米.(结果保留整数,参考数值:| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com