
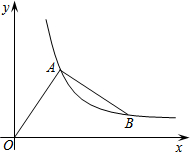
 如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则$\frac{b}{a}$的值等于$\frac{1+\sqrt{5}}{2}$.
如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则$\frac{b}{a}$的值等于$\frac{1+\sqrt{5}}{2}$. 分析 过A作AE⊥x轴,过B作BD⊥AE,利用同角的余角相等得到一对角相等,再由一对直角相等,且AO=AB,利用AAS得出三角形AOE与三角形ABD全等,由确定三角形的对应边相等得到BD=AE=b,AD=OE=a,进而表示出ED及OE+BD的长,即可表示出B坐标;由A与B都在反比例图象上,得到A与B横纵坐标乘积相等,列出关系式,变形后即可求出$\frac{b}{a}$的值.
解答  解:过A作AE⊥x轴,过B作BD⊥AE,
解:过A作AE⊥x轴,过B作BD⊥AE,
∵∠OAB=90°,
∴∠OAE+∠BAD=90°,
∵∠AOE+∠OAE=90°,
∴∠BAD=∠AOE,
在△AOE和△BAD中,
$\left\{\begin{array}{l}{∠AOE=∠BAD}\\{∠AEO=∠BDA=90°}\\{AO=BA}\end{array}\right.$,
∴△AOE≌△BAD(AAS),
∴AE=BD=b,OE=AD=a,
∴DE=AE-AD=b-a,OE+BD=a+b,
则B(a+b,b-a);
∵A与B都在反比例图象上,得到ab=(a+b)(b-a),
整理得:b2-a2=ab,即($\frac{b}{a}$)2-$\frac{b}{a}$-1=0,
∵△=1+4=5,
∴$\frac{b}{a}$=$\frac{1±\sqrt{5}}{2}$,
∵点A(a,b)为第一象限内一点,
∴a>0,b>0,
则$\frac{b}{a}$=$\frac{1+\sqrt{5}}{2}$.
故答案为$\frac{1+\sqrt{5}}{2}$.
点评 此题属于反比例函数综合题,涉及的知识有:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形的性质,以及一元二次方程的解法,熟练掌握反比例函数的性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
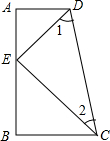 如图,CB⊥AB于点B,DA⊥AB于点A,CE平分∠BCD,DE平分∠CDA,点E在AB上,请问:∠1和∠2有何等量关系?并证明你的结论.
如图,CB⊥AB于点B,DA⊥AB于点A,CE平分∠BCD,DE平分∠CDA,点E在AB上,请问:∠1和∠2有何等量关系?并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com