
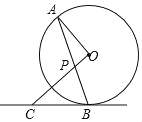
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若OA=5,OP=3,求CB的长;
(3)设△AOP的面积是S1,△BCP的面积是S2,且![]() .若⊙O的半径为4,BP=
.若⊙O的半径为4,BP=![]() ,求tan∠CBP.
,求tan∠CBP.
【答案】(1)见解析;(2)2
【解析】
(1)连接OB,由OP⊥OA,得∠A+∠APO=90°;由CP=CB,得∠CBP=∠CPB;再由OA=OB,得∠A=∠OBA,而∠CPB=∠APO,整理变形可得∠OBC=90°,即BC是⊙O的切线;
(2)设BC=x,则PC=x,在Rt△OBC中,由勾股定理可得关于x的方程
52+x2=(x+3)2,解方程即可求出CB的长;
(3)作CD⊥BP于D,由PC=PB,得PD=BD=![]() PB=
PB=![]() ,易证△AOP∽△PCD,则由
,易证△AOP∽△PCD,则由![]() ,可得
,可得![]() ,即
,即![]() ,由此可求CD的长,再在Rt△BCD中,按照正切定义求出tan∠CBP即可.
,由此可求CD的长,再在Rt△BCD中,按照正切定义求出tan∠CBP即可.
(1)证明:连接OB,如图,
∵OP⊥OA,
∴∠AOP=90°,
∴∠A+∠APO=90°,
∵CP=CB,
∴∠CBP=∠CPB,
而∠CPB=∠APO,
∴∠APO=∠CBP,
∵OA=OB,
∴∠A=∠OBA,
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:设BC=x,则PC=x,
在Rt△OBC中,OB=OA=5,OC=CP+OP=x+3,
∵OB2+BC2=OC2,
∴52+x2=(x+3)2,
解得x=![]() ,
,
即BC的长为![]() ;
;
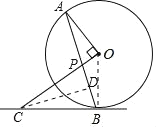
(3)解:如图,作CD⊥BP于D,
∵PC=PB,
∴PD=BD=![]() PB=
PB=![]() ,
,
∵∠PDC=∠AOP=90°,∠APO=∠CPD,
∴△AOP∽△PCD,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OA=4,
∴CD=![]() ,
,
∴tan∠CBP=![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
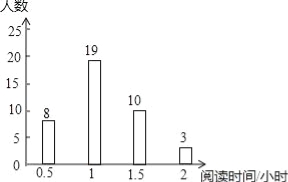
A.2和1 B.1.25和1 C.1和1 D.1和1.25
查看答案和解析>>
科目:初中数学 来源: 题型:
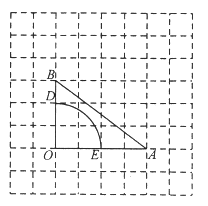
【题目】如图,在每个小正方形的边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均在格点上,点
均在格点上,点![]() 在
在![]() 上,且点
上,且点![]() 也在格点上.
也在格点上.
(Ⅰ)![]() 的值为_____________;
的值为_____________;
(Ⅱ)![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的一段圆弧.在如图所示的网格中,将线段
为半径的一段圆弧.在如图所示的网格中,将线段![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为,连接
,旋转角为,连接![]() ,
,![]() ,当
,当![]() 的值最小时,请用无刻度的直尺画出点
的值最小时,请用无刻度的直尺画出点![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心____点,按顺时针方向旋转___度得到;
(3)若BC=8,DE=2,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD 中AB=8![]() ,AD=10,点 E 是 CD 的中点,将这张纸片依次折叠两次: 第一次折叠纸片使点 A 与点 E 重合,如图 2,折痕为 MN,连接 ME、NE;第二次折叠纸片使点 N 与点 E 重合,如图 3,点 B 落到 B′处,折痕为 HG,连接 HE,则下列结论正确的个数是( )①ME∥HG;②△MEH 是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点 E 是 CD 的中点,将这张纸片依次折叠两次: 第一次折叠纸片使点 A 与点 E 重合,如图 2,折痕为 MN,连接 ME、NE;第二次折叠纸片使点 N 与点 E 重合,如图 3,点 B 落到 B′处,折痕为 HG,连接 HE,则下列结论正确的个数是( )①ME∥HG;②△MEH 是等边三角形;③∠EHG=∠AMN;④tan∠EHG=![]() ;
;

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学社团小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点在一条直线上,请根据以上数据计算GH的长(![]() =1.73,要求结果精确得到0.1m)
=1.73,要求结果精确得到0.1m)
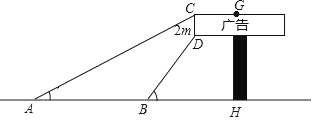
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
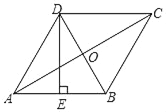
A. 18 B. 18![]() C. 9
C. 9![]() D. 6
D. 6![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com