
��ͼ��������y=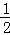 x2��
x2��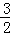 x��9��x�ύ��A��B���㣬��y�ύ�ڵ�C������BC��AC��
x��9��x�ύ��A��B���㣬��y�ύ�ڵ�C������BC��AC��
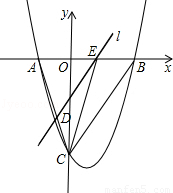
��1����AB��OC�ij���
��2����E�ӵ�A��������x�����B�˶�����E���A��B���غϣ�������E��ֱ��lƽ��BC����AC�ڵ�D����AE�ij�Ϊm����ADE�����Ϊs����s����m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3���ڣ�2���������£�����CE�����CDE��������ֵ����ʱ������Ե�EΪԲ�ģ���BC���е�Բ���������������У���
��1��AB=9��OC=9 ��2��s= m2��0��m��9��
��3��S��E=
m2��0��m��9��
��3��S��E=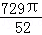
��������
����������⣺��1����֪��������y= x2��
x2��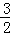 x��9��
x��9��
��x=0ʱ��y=��9����C��0����9����
��y=0ʱ�� x2��
x2��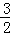 x��9=0���ã�x1=��3��x2=6����A����3��0����B��6��0����
x��9=0���ã�x1=��3��x2=6����A����3��0����B��6��0����
��AB=9��OC=9��
��2����ED��BC��
���AED�ס�ABC��
�� =��
=�� ��2������
��2������ =��
=�� ��2���ã�s=
��2���ã�s= m2��0��m��9����
m2��0��m��9����
��3��S��AEC= AE?OC=
AE?OC= m��S��AED=s=
m��S��AED=s= m2��
m2��
��S��EDC=S��AEC��S��AED=�� m2+
m2+ m=��
m=�� ��m��
��m�� ��2+
��2+ ��
��
���CDE��������Ϊ ����ʱ��AE=m=
����ʱ��AE=m= ��BE=AB��AE=
��BE=AB��AE= ��
��
��E��EF��BC��F����R t ��BEF��R t ��BCO���ã�
 =
= ������
������ =
=
��EF= ��
��
����E��ΪԲ�ģ���BC���е�Բ����� S��E=��?EF2=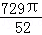 ��
��

���㣺���κ���ͼ���뼸��ͼ�ν��
�������������⣬��Խ��ѣ��dz����⣬����ѧ���Զ��κ���ͼ�������ߡ���������Ľ������գ���ص�������뼸��ͼ�α߳��Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
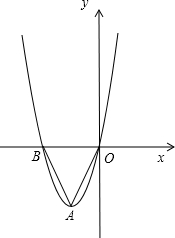 ��ͼ��������y=x2+4x��x��ֱ��ཻ�ڵ�B��O�����Ķ���ΪA������AB��AO��
��ͼ��������y=x2+4x��x��ֱ��ཻ�ڵ�B��O�����Ķ���ΪA������AB��AO���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 16����ͼ��������y=-x2+2x+m��m��0����x���ཻ�ڵ�A��x1��0����B��x2��0������A�ڵ�B����࣮��x=x2-2ʱ��y
16����ͼ��������y=-x2+2x+m��m��0����x���ཻ�ڵ�A��x1��0����B��x2��0������A�ڵ�B����࣮��x=x2-2ʱ��y�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪��ͼ��������y=x2+��k2+1��x+k+1�ĶԳ�����ֱ��x=-1���Ҷ�����x���Ϸ�����M��ֱ��x=-1����������ϵ�һ���㣬����M��x��Ĵ���MG������ΪG������M��ֱ��x=-1�Ĵ���MN������ΪN��ֱ��x=-1��x��Ľ���H�㣬��M��ĺ�����Ϊx������MNHG���ܳ�Ϊl��
��֪��ͼ��������y=x2+��k2+1��x+k+1�ĶԳ�����ֱ��x=-1���Ҷ�����x���Ϸ�����M��ֱ��x=-1����������ϵ�һ���㣬����M��x��Ĵ���MG������ΪG������M��ֱ��x=-1�Ĵ���MN������ΪN��ֱ��x=-1��x��Ľ���H�㣬��M��ĺ�����Ϊx������MNHG���ܳ�Ϊl���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•���ݣ���ͼ��������y=x2-2x-8��y���ڵ�A����x���������ڵ�B��
��2013•���ݣ���ͼ��������y=x2-2x-8��y���ڵ�A����x���������ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
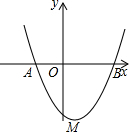 ��ͼ��������y=x2-2x-3��x��ֱ���A��B���㣮
��ͼ��������y=x2-2x-3��x��ֱ���A��B���㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com