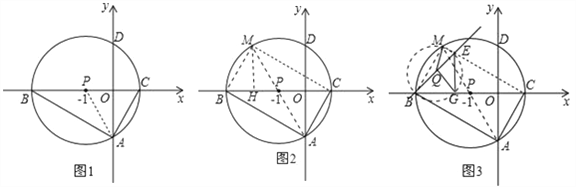
【题目】如图，以点P（﹣1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=2，将△ABC绕点P旋转180°，得到△MCB．

（1）求B、C两点的坐标；

（2）请在图中画出线段MB、MC，并判断四边形ACMB的形状（不必证明），求出点M的坐标；

（3）动直线l从与BM重合的位置开始绕点B顺时针旋转，到与BC重合时停止，设直线l与CM交点为E，点Q为BE的中点，过点E作EG⊥BC于G，连接MQ、QG．请问在旋转过程中∠MQG的大小是否变化？若不变，求出∠MQG的度数；若变化，请说明理由．

参考答案：

【答案】（1）B（﹣﹣1，0），C（﹣1，0）；

（2）（﹣2，1）；

（3）∠MQG的大小不变，始终等于135°,理由见解析．

【解析】试题分析：（1）连接PA，运用垂径定理及勾股定理即可求出圆的半径，从而可以求出B、C两点的坐标．

（2）由于圆P是中心对称图形，显然射线AP与圆P的交点就是所需画的点M，连接MB、MC即可；易证四边形ACMB是矩形；过点M作MH⊥BC，垂足为H，易证△MHP≌△AOP，从而求出MH、OH的长，进而得到点M的坐标．

（3）易证点E、M、B、G在以点Q为圆心，QB为半径的圆上，从而得到∠MQG=2∠MBG．由等腰直角三角形和等腰三角形的性质得出∠PCA=67.5°，从而得到∠MBG=67.5°，进而得到∠MQG=135°，即∠MQG的度数是定值．

试题解析：解：（1）连接PA，如图1所示．

∵PO⊥AD，∴AO=DO．

∵AD=2，∴OA=1．

∵点P坐标为（﹣1，0），∴OP=1，∴PA=== ，∴BP=CP=，∴OB=+1，OC=﹣1，∴B（﹣﹣1，0），C（﹣1，0）．

（2）连接AP，延长AP交⊙P于点M，连接MB、MC．

如图2所示，线段MB、MC即为所求作．

四边形ACMB是矩形．理由如下：

∵△MCB由△ABC绕点P旋转180°所得，∴四边形ACMB是平行四边形．

∵BC是⊙P的直径，∴∠CAB=90°，∴平行四边形ACMB是矩形．

过点M作MH⊥BC，垂足为H，如图2所示．

在△MHP和△AOP中，∵∠MHP=∠AOP，∠HPM=∠OPA，PM=PM，∴△MHP≌△AOP（AAS），∴MH=OA=1，PH=PO=1，∴OH=2，∴点M的坐标为（﹣2，1）．

（3）在旋转过程中∠MQG的大小不变．

∵四边形ACMB是矩形，∴∠BMC=90°．

∵EG⊥BO，∴∠BGE=90°，∴∠BMC=∠BGE=90°．

∵点Q是BE的中点，∴QM=QE=QB=QG，∴点E、M、B、G在以点Q为圆心，QB为半径的圆上，如图3所示，∴∠MQG=2∠MBG．

∵OA=OP=1，∠AOP=90°，∴∠APC=45°，∵PC=PA，∴∠PCA=∠PAC=（180°-45°）=67.5°，∴∠MBC=∠BCA=67.5°，∴∠MQG=135°，∴在旋转过程中∠MQG的大小不变，始终等于135°．

关闭