Question

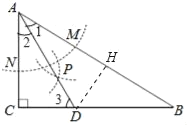
【题目】如图，在△ABC中，∠C＝90°，∠B＝30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连接AP，并廷长交BC于点D，则下列说法中正确的个数是（　　）

①AD是∠BAC的平分线

②∠ADC＝60°

③点D在AB的垂直平分线上

④若AD＝2dm，则点D到AB的距离是1dm

⑤S△DAC：S△DAB＝1：2

A.2B.3C.4D.5

Answer 1

【答案】D

【解析】

①根据作图的过程可以判定AD是∠BAC的角平分线；
②利用角平分线的定义可以推知∠CAD=30°，则由直角三角形的性质来求∠ADC的度数；
③利用等角对等边可以证得△ADB的等腰三角形，由等腰三角形的“三线合一”的性质可以证明点D在AB的中垂线上；
④作DH⊥AB于H，由∠1=∠2，DC⊥AC，DH⊥AB，推出DC=DH即可解决问题；
⑤利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比．

解：①根据作图的过程可知，AD是∠BAC的平分线，故①正确；

②如图，∵在△ABC中，∠C＝90°，∠B＝30°，

∴∠CAB＝60°．

又∵AD是∠BAC的平分线，

∴∠1＝∠2＝∠CAB＝30°，

∴∠3＝90°﹣∠2＝60°，即∠ADC＝60°．故②正确；

③∵∠1＝∠B＝30°，

∴AD＝BD，

∴点D在AB的中垂线上．故③正确；

④作DH⊥AB于H，

∵∠1＝∠2，DC⊥AC，DH⊥AB，

∴DC＝DH，

在Rt△ACD中，CD＝AD＝1dm，

∴点D到AB的距离是1dm；故④正确，

⑤在Rt△ACB中，∵∠B＝30°，

∴AB＝2AC，

∴S△DAC：S△DAB＝ACCD：ABDH＝1：2；故⑤正确．

综上所述，正确的结论是：①②③④⑤，共有5个．

故选：D．