
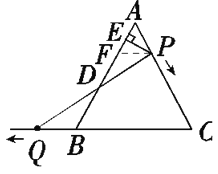
����Ŀ����ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ�P��AC����һ���㣬��A��C�˶�����A��C���غϣ���Q��CB�ӳ�����һ���㣬���Pͬʱ����ͬ���ٶ���B��CB�ӳ��߷����˶���Q����B�غϣ�����P��PE��AB��E������PQ��AB��D��
��1����AE=1ʱ����AP�ij���
��2������BQD=30��ʱ����AP�ij���
��3�����˶��������߶�ED�ij��Ƿ����仯��������䣬����߶�ED�ij�����������仯����˵������.

���𰸡���1��2����2��2����3��DE=3������.
�������������������1���ɡ�APF�ǵȱ���������PE��AF���õ���APE=30�㣬��30������ֱ�DZߵ���б�ߵ�һ�룬�õ����ۣ�
��2����P��PF��QC������AFP�ǵȱ������Σ��ɵõ���DBQ�ա�DFP���õ���BQD=��BDQ=��FDP=��FPD=30�㣬�õ�BD=DF=FA���Ӷ��õ����ۣ�
��3���ɣ�2���õ�BD=DF���õ�DE+DF+EF=AB=6���Ӷ��õ�DE=3��Ϊ��ֵ��
����������⣺��1���ߡ�APF�ǵȱ������������A=60������PE��AF�����APE=30����
��AE=1����APE=30����PE��AF����AP=2AE=2��
��2����![]() ��PF��QC������AFP�ǵȱ������Σ�
��PF��QC������AFP�ǵȱ������Σ�
��![]() ͬʱ�������ٶ���ͬ����
ͬʱ�������ٶ���ͬ����![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��![]()
��![]()
![]()
��3���ɣ�2��֪![]() ����
����![]() �ǵȱ������Σ�
�ǵȱ������Σ� ![]() ��
��
��![]()
![]() ��
��![]()
��![]() Ϊ��ֵ����
Ϊ��ֵ����![]() �ij�������
�ij�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��cΪ��ABC�����ߣ������㣨a��b����a2+b2��c2��=0������ABC���� ��
A. �ȱ������� B. ֱ��������
C. ����ֱ�������� D. ���������λ�ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ����ڡ����ҹ��Ŵ���������ѧ�����������������е�һ�����⣬������Բ�ģ����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��ʾ⼸�Σ������ִ�����ѧ���Ա����ǣ�����ͼ��CDΪ��O��ֱ������AB��CD����ΪE��CE=1�磬AB=10�磬��ֱ��CD�ij����������⣬CD��Ϊ�� ��

A��12�� B��13�� C��24�� D��26��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��x��2x��y������x+y����x��y��+��x��y��2 �� ����x2+y2=5��xy=��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A����8��3����B����4��0����C����4��3������ABC=������������y=![]() x2+bx+c������C���ҶԳ���Ϊx=��
x2+bx+c������C���ҶԳ���Ϊx=��![]() ������y�ύ�ڵ�G��
������y�ύ�ڵ�G��
��1���������ߵĽ���ʽ����G�����ꣻ
��2����Rt��ABC��x������ƽ��m����λ��ʹB���Ƶ���E��Ȼ���������Ƶ�E˳ʱ����ת�����õ���DEF������Fǡ�������������ϣ�����m��ֵ��
������CG��x���ڵ�H������FG����B��BP��FG����CG�ڵ�P����֤��PH=GH��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y=��![]() x��ͼ���뷴��������y=
x��ͼ���뷴��������y=![]() ��ͼ��ֱ���M��N���㣬��֪��M����2��m����
��ͼ��ֱ���M��N���㣬��֪��M����2��m����
��1�����������ı���ʽ��
��2����PΪy���ϵ�һ�㣬����MPNΪֱ��ʱ��ֱ��д����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������߶���a=3��b=5��cΪ��������ô��a��b��cΪ����ɵ������ι�����������
A. 1�� B. 3�� C. ������� D. ��ȷ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com