
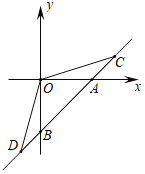
【题目】如图,直线l:y=x﹣2分别交x,y轴于A、B两点,C、D是直线l上的两个动点,点C在第一象限,点D在第三象限.且始终有∠COD=135°.
(1)求证:△OAC∽△DBO;
(2)若点C、D都在反比例函数y=![]() 的图象上,求k的值;
的图象上,求k的值;
(3)记△OBD的面积为S1,△AOC的面积为S2,且![]() =
=![]() ,二次函数y=ax2+bx+c满足以下两个条件:①图象过C、D两点;②当S1
,二次函数y=ax2+bx+c满足以下两个条件:①图象过C、D两点;②当S1![]() x
x![]() S2时,y有最大值2,求a的值.
S2时,y有最大值2,求a的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先求出点A,点B坐标,可求∠OAB=∠OBA=45°,由外角的性质可求∠DOB=∠ACO,∠AOC=∠ODB,可证△OAC∽△DBO;
(2)由相似三角形的性质可得![]() ,设
,设![]() =a>0,用a表示点C,点D坐标,代入反比例函数解析式,可求解;
=a>0,用a表示点C,点D坐标,代入反比例函数解析式,可求解;
(3)先求出点C,点D坐标,代入解析式,由题意可得当x=2时,y有最大值2,组成方程组,可求a的值.
解:(1)∵直线l:y=x﹣2分别交x,y轴于A、B两点,
∴点A(2,0),点B(0,﹣2),
∴AO=BO=2,
∴∠OAB=∠OBA=45°,
∴∠OCA+∠AOC=45°,∠ODB+∠DOB=45°,
∵∠COD=135°,
∴∠DOB+∠AOB+∠AOC=135°,
∴∠DOB+∠AOC=45°,
∴∠DOB=∠ACO,∠AOC=∠ODB,
∴△OAC∽△DBO;
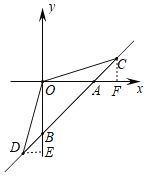
(2)如图,过点C作CF⊥x轴于F,过点D作DE⊥y轴于E,
∵△OAC∽△DBO,
∴![]() ,
,
∴设![]() =a>0,
=a>0,
∴BD=![]() ,AC=2a,
,AC=2a,
∵∠CAF=∠OAB=45°,
∴∠ACF=∠CAF=45°,
∴AF=CF=![]() =
=![]() a,
a,
∴点C坐标(2+![]() a,
a,![]() a),
a),
同理可求点D坐标(﹣![]() ,﹣2﹣
,﹣2﹣![]() ),
),
∵点C、D都在反比例函数y=![]() 的图象上,
的图象上,
∴(2+![]() a)
a)![]() a=
a=![]() (2+
(2+![]() )
)
∴(![]() a2+2a+
a2+2a+![]() )(a+1)(a﹣1)=0,
)(a+1)(a﹣1)=0,
∵a>0,
∴![]() a2+2a+
a2+2a+![]() ≠0,a+1≠0,
≠0,a+1≠0,
∴a﹣1=0,
∴点C(2+![]() ,
,![]() )
)
∴k=![]() (2+
(2+![]() )=
)=![]() ;
;
(3)∵△OAC∽△DBO,
∴![]() ,
,
∴![]() ,
,
∴AC=2![]() ,
,
∴AF=CF=2,
∴点C(4,2),
∵![]() ,
,
∴![]() ,
,
∴BD=![]() ,
,
∴DE=BE=1,
∴点D(﹣1,﹣3),
∴△OBD的面积为S1=![]() ×2×1=1,△AOC的面积为S2=
×2×1=1,△AOC的面积为S2=![]() ×2×2=2,
×2×2=2,
∵二次函数y=ax2+bx+c满足以下两个条件:①图象过C、D两点;②当1≤x≤2时,y有最大值2,
∴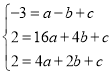 ,
,
解得: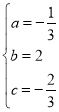 ,
,
∴a=![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
【题目】2020年初,一场突如其来的疫情,让本该回到学校的学子们宅在家里上网课.为了解学生对网课的满意度,某校随机抽取了部分学生进行调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整),请根据图中信息回答问题:

(1)求被随机抽取的学生数及m的值,并补全条形统计图.
(2)在扇形统计图中,求满意度为“非常不满意”所对应的扇形圆心角的度数.
(3)若该校共有学生3000人,估计上网课满意度为“非常满意”和“满意”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】报刊零售点从报社以每份0.30元买进一种晚报,零售点卖出的价格为0.50元,约定卖不掉的报纸可以退还给报社,退还的钱数y(元)与退还的报纸数量k(份)之间的函数关系式如下:当0≤k<30时, y=![]() ;当k≥30时,y=0.02k,现经市场调查发现,在一个月中(按30天记数)有20天可卖出150份/天,有10天只能卖出100份/天,而报社规定每天批发给摊点的报纸的数量必须相同.
;当k≥30时,y=0.02k,现经市场调查发现,在一个月中(按30天记数)有20天可卖出150份/天,有10天只能卖出100份/天,而报社规定每天批发给摊点的报纸的数量必须相同.
(1)若该家报刊摊点每天从报社买进的报纸数x份(满足100<x≤150),月毛利润为W元,求W关于x的函数关系式;
(2)当买进多少报纸时,月毛利润最大?为多少?(注:月毛利润=月总销售额-月总成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“停课不停学”期间,学生对线上学习方式的偏好情况,某校随机抽取40名学生进行问卷调查,其统计结果如表:
最喜欢的线上学习方式(每人最多选一种) | 人数 |
直播 | 10 |
录播 | a |
资源包 | 5 |
线上答疑 | 8 |
合计 | 40 |
(1)a= ;
(2)若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图,求“直播”对应扇形的圆心角度数;
(3)根据调查结果估计该校1000名学生中,最喜欢“线上答疑”的学生人数;
(4)在最喜欢“资源包”的学生中,有2名男生,3名女生.现从这5名学生中随机抽取2名学生介绍学习经验,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校想知道九年级学生对我国倡导的“一带一路”的了解程度,随机抽取部分九年级学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):A.非常了解.B.了解.C.知道一点.D.完全不知道.将调查的结果绘制如下两幅不完整的统计图,请根据两幅统计图中的信息,解答下列问题:
(1)求本次共调查了多少学生?
(2)补全条形统计图;
(3)该校九年级共有600名学生,请你估计“了解”的学生约有多少名?
(4)在“非常了解”的3人中,有2名女生,1名男生,老师想从这3人中任选两人做宣传员,请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
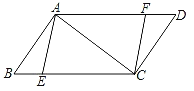
【题目】如图,在ABCD中,BC=10,对角线AC⊥AB,点EF在BC、AD上,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)当四边形AECF是菱形时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校全体学生积极参加校团委组织的“献爱心捐款”活动,为了解捐款情况,随机抽取了部分学生并对他们的捐款情况作了统计,绘制了两幅不完整的统计图(统计图中每组含最小值,不含最大值).请依据图中信息解答下列问题:

(1)求随机抽取的学生人数;
(2)填空:(直接填答案)
①“20元~25元”部分对应的圆心角度数为______;
②捐款的中位数落在______(填金额范围);
(3)若该校共有学生3500人,请估算全校捐款不少于20元的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的提高和环境的不断改善,带动了旅游业的发展.某市旅游景区有A,B,C,D四个著名景点,该市旅游部门统计绘制出2019年游客去各景点情况统计图,根据给出的信息解答下列问题:
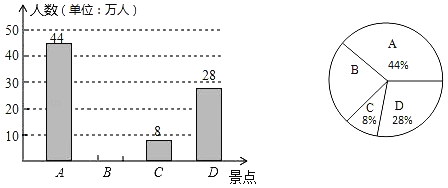
(1)2019年该市旅游景区共接待游客 万人,扇形统计图中C景点所对应的圆心角的度数是 度;
(2)把条形统计图补充完整;
(3)甲,乙两位同学去该景区旅游,用树状图或列表法,求甲,乙两位同学在A,B,D三个景点中,同时选择去同一景点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
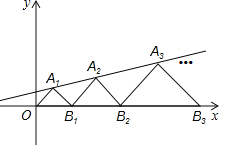
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,
,![]() ,…和
,…和![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上.
轴上.![]() ,
,![]() ,
,![]() ,…都是等腰直角三角形,它们的面积分别记作
,…都是等腰直角三角形,它们的面积分别记作![]() ,
,![]() ,
,![]() ,…,如果点
,…,如果点![]() 的坐标为
的坐标为![]() ,那么
,那么![]() 的纵坐标为_______.
的纵坐标为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com