
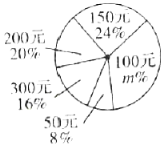
����Ŀ��2020�����һ��ͻ�����������飬�ñ��ûص�ѧУ��ѧ����լ�ڼ��������Σ�Ϊ�˽�ѧ�������ε�����ȣ�ijУ�����ȡ�˲���ѧ�����е��飨ÿ�˱�����ֻѡ����һ�������ͳ�ƽ�����Ƴ�����ͳ��ͼ�����������������ͼ����Ϣ�ش����⣺

��1���������ȡ��ѧ������m��ֵ������ȫ����ͳ��ͼ��
��2��������ͳ��ͼ�У��������Ϊ���dz������⡱����Ӧ������Բ�ĽǵĶ�����
��3������У����ѧ��3000�ˣ����������������Ϊ���dz����⡱�͡����⡱��ѧ�����ж����ˣ�
���𰸡���1��36������������2��18������3��1410��
��������
��1����A����������ٷ��ʣ����ɵõ���ȡ��ѧ������Ȼ�����m��ֵ���ٲ�ȫ����ͼ���ɣ�
��2������E��İٷֱȳ���360�����ɵõ�Բ�ĽǵĶ�����
��3������������������ٷ��ʣ����ɵõ��𰸣�
�⣺��1���������ȡ��ѧ������11��11%��100�ˣ�
![]()
��m��36��
��ȫͳ��ͼ���£�

��2��Բ�Ľǣ�5��100��360����18����
��3�����������������Ϊ���dz�������������������ѧ������
3000����11%+36%����1410�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
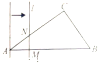
����Ŀ����ͼ����֪�ı���AECF��ƽ���ı��Σ�D��B�ֱ���AF��CE���ӳ����ϣ�����AB��CD������B=��D��
��֤����1����ABE�ա�CDF��
��2���ı���ABCD��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ܹ������人���飬ij��˾ͨ���人�д����ܻ��ά����人�����ݾ������Ƴɲ�����������ͳ��ͼ��ͼ1��������ͳ��ͼ��ͼ2����

ͼ1 ͼ2
��1������������Ϣ��֪�μӾ��������Ϊ______��![]() ______���������λ��Ϊ______���벹ȫ����ͳ��ͼ��
______���������λ��Ϊ______���벹ȫ����ͳ��ͼ��
��2�����Ӿ������У����ѡһ�˴�����˾ȥ������˾�������������ѡ�о�����![]() Ԫ���˵ĸ��ʣ�
Ԫ���˵ĸ��ʣ�
��3����������˾�м��˲����˾�������¾������ԭ������ϲ���һ�������ݣ��������������ı䣬����������м��˲����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=10��AC=8��BC=6��ֱ��l������A���Ҵ�ֱ��AB���ֱ���AB��AC�ཻ�ڵ�M��N��ֱ��l�ӵ�A��������AB������1cm/s���ٶ����B�˶�����ֱ��l������Bʱֹͣ�˶������˶���������AMN�������y(cm2)��ֱ��l���˶�ʱ����x(s)��y��x֮�亯����ϵ��ͼ�������( )
A.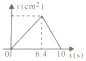 B.
B.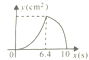
C.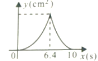 D.
D.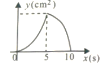
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
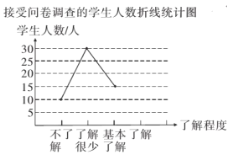
����Ŀ����У��������һ�������¹ڷ���ר��ѧ���ֳ�������֪��ͬѧ�Ƕ��¹ڷ���֪ʶ���˽�̶ȣ����������ȡ����ͬѧ���д��ʾ����飬�������ռ�������Ϣ������ͳ�ƣ������������������в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1�������ʾ������ͬѧ���� ����
��2���벹ȫ����ͳ��ͼ�����������ͳ��ͼ�С������˽⡱��������Ӧ���ε�Բ�ĽǵĴ�С��
��3��Ϊ����ȫУʦ�����ܸ��õ�Ԥ���¹ڷ��ף�ѧ��������֯һ������������ʾ������С��˽⡱�ļ���ͬѧ���һ�������ţ���֪�⼸��ͬѧ��ֻ������Ů������Ҫ�ڸ�����������ѡ����ͬѧ��ȫУʦ����������������ԣ������б�����״ͼ�ķ�������ѡȡ������ͬѧ����Ů���ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
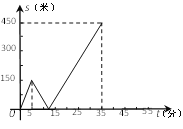
����Ŀ�������������ٴ�ͬһ�ص㵽1500�״���ͼ��ݿ��飬�׳���5���Ӻ�����50��/�ֵ��ٶ���ͬһ·������.������������![]() ���ף��������ߵ�ʱ��Ϊ
���ף��������ߵ�ʱ��Ϊ![]() ���֣���
���֣���![]() ����
����![]() �ĺ�������ͼ���һ������ͼ��ʾ.
�ĺ�������ͼ���һ������ͼ��ʾ.
��1��������ߵ��ٶȣ�
��2��������ϵ�У�����![]() ����
����![]() ����ͼ������ಿ�֣�
����ͼ������ಿ�֣�
��3���ʼס������˺�ʱ���360�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ѡ����ͬѧ�μ�����ʡ��Ӣ����˵����������ij��ѧ�����ˡ�Ӣ�ﵥ����д��������ÿλѧ����д����99�������������������鲿��ѧ������д����������Ǹ��ݳ�������Ƶ�ͳ��ͼ��һ���֣�
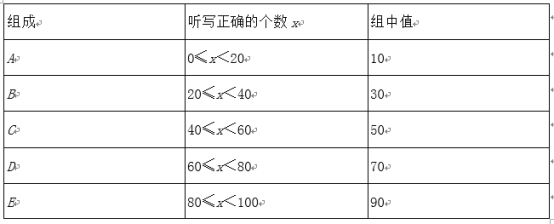
����������Ϣ����������⣺
��1�����ι����������� ����ѧ��������ȫƵ���ֲ�ֱ��ͼ��
��2������ÿ����д��ȷ�ĸ������������ݵ�����ֵ���棬���ѧ����д��ȷ�ĸ�����ƽ�����Ƕ��٣�
��3����У����3000��ѧ���������д��ȷ�ĸ�������60����Ϊ���ϸ������������ѧУ���ξ�����д���ϸ��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��ABC��ƽ���߽���O�ڵ�D��DE��BC�ڵ�E��
��1�����ж�DE���O��λ�ù�ϵ����˵�����ɣ�
��2������D��DF��AB�ڵ�F����BE=3![]() ��DF=3����ͼ����Ӱ���ֵ������
��DF=3����ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
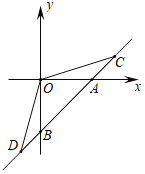
����Ŀ����ͼ��ֱ��l��y��x��2�ֱ�x��y����A��B���㣬C��D��ֱ��l�ϵ��������㣬��C�ڵ�һ���ޣ���D�ڵ������ޣ���ʼ���С�COD��135����
��1����֤����OAC�ס�DBO��
��2������C��D���ڷ���������y��![]() ��ͼ���ϣ���k��ֵ��
��ͼ���ϣ���k��ֵ��
��3������OBD�����ΪS1����AOC�����ΪS2����![]() ��
��![]() �����κ���y��ax2+bx+c��������������������ͼ���C��D���㣻�ڵ�S1
�����κ���y��ax2+bx+c��������������������ͼ���C��D���㣻�ڵ�S1![]() x
x![]() S2ʱ��y�����ֵ2����a��ֵ��
S2ʱ��y�����ֵ2����a��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com