
����Ŀ�����ⱳ�����ڡ�ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ![]() ������������ε������С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�����㣨���������㶼��С�����εĶ��㴦������ͼ��ʾ����������Ҫ��ߣ�������������ܼ��������������뽫��ABC�����ֱ����д�ں������� ����
������������ε������С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�����㣨���������㶼��С�����εĶ��㴦������ͼ��ʾ����������Ҫ��ߣ�������������ܼ��������������뽫��ABC�����ֱ����д�ں������� ����
˼ά��չ�����ǰ��������ABC����ķ���������ͼ��������ABC�У�AB��BC��AC���߳��ֱ�Ϊ![]() ��2
��2![]() ��a��0����������ͼ��������������ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC��ֱ��д��������������ϵĸ����� ����
��a��0����������ͼ��������������ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC��ֱ��д��������������ϵĸ����� ����

���𰸡����ⱳ���� ![]() ��˼ά��չ��
��˼ά��չ�� ![]() a��
a��
��������
���ⱳ�������ݷָ�������ε������
˼ά��չ��![]() a��ֱ�DZ߳�Ϊa��2a��ֱ�������ε�б�ߣ�2
a��ֱ�DZ߳�Ϊa��2a��ֱ�������ε�б�ߣ�2![]() ��ֱ�DZ߳�Ϊ2a��2a��ֱ�������ε�б�ߣ�
��ֱ�DZ߳�Ϊ2a��2a��ֱ�������ε�б�ߣ�![]() ��ֱ�DZ߳�Ϊa��4a��ֱ�������ε�б�ߣ���������Ϊһ�����ε������ȥ����ֱ�������ε����������ͼ��BH��AC��H�������������⼴�ɣ�
��ֱ�DZ߳�Ϊa��4a��ֱ�������ε�б�ߣ���������Ϊһ�����ε������ȥ����ֱ�������ε����������ͼ��BH��AC��H�������������⼴�ɣ�
�⣺���ⱳ����S��ABC��3��3��![]() ��1��2��
��1��2��![]() ��1��3��
��1��3��![]() ��2��3��
��2��3��![]() ��
��
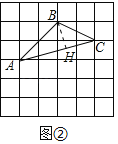
˼ά��չ����ͼ��BH��AC��H��
��S��ABC��![]() ACBH��2a��4a��
ACBH��2a��4a��![]() ��2a��2a��
��2a��2a��![]() ��a��2a��
��a��2a��![]() ��a��4a��3a2��
��a��4a��3a2��
��![]() ��
��![]() a��BH��3a2��
a��BH��3a2��
��BH��![]() a��
a��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB����O��ֱ������C����O�ϣ�����C��ֱ����AB���ӳ��߽��ڵ�P��AC=PC����COB=2��PCB.

��1����֤��PC����O�����ߣ�
��2����֤��BC=![]() AB��
AB��
��3����M�ǻ�AB���е㣬CM��AB�ڵ�N����AB=4����MN![]() MC��ֵ.
MC��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�����ߣ�AE��BC��BE��AD�ڵ�F����AC��G��F��AD���е�.
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2����EB�ǡ�AEC�Ľ�ƽ���ߣ���д��ͼ��������AE��ȵı�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��![]()
��2����֪![]() ����
����![]() ��ֵ
��ֵ
��3��(x+y-z)(x-y+z)
��4��[(x+2y)(x-2y)-(x+4y)2]��4y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڳ���һ�����������������¶Ȳ���ʱ���������������ѹp��kPa�����������V��m3���ķ�������������ͼ����ͼ��ʾ��

��1��д����һ�����ı���ʽ��
��2�����������Ϊ1 m3ʱ����ѹ�Ƕ��٣�
��3���������ڵ���ѹ����140 kPaʱ������ը��Ϊ�˰�ȫ��������������Ӧ��С�ڶ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��x��0����ͼ����A��2
��x��0����ͼ����A��2![]() ��1����ֱ��AB�뷴��������ͼ������һ��B��1��a��������AC��y�ύ�ڵ�C����BAC=75�㣬AD��y�ᣬ����ΪD��
��1����ֱ��AB�뷴��������ͼ������һ��B��1��a��������AC��y�ύ�ڵ�C����BAC=75�㣬AD��y�ᣬ����ΪD��
��1�����������Ľ���ʽ��
��2����tan��DAC��ֵ��ֱ��AC�Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���мƻ������ס���������Ʒ��������Ʒ�Ľ��ۡ��ۼ����±���
��Ʒ | �� | �� |
���ۣ�Ԫ/���� |
|
|
�ۼۣ�Ԫ/���� | 200 | 100 |
����360Ԫ����������Ʒ�ļ�������180Ԫ����������Ʒ�ļ�����ͬ��
��1����ס���������Ʒ�Ľ����Ƕ���Ԫ��
��2�����������ۼס���������Ʒ��50�����������ۼ�����ƷΪ![]() ����
����![]() ������������50���ס���������Ʒ��������Ϊ
������������50���ס���������Ʒ��������Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() ֮��ĺ�����ϵʽ�������
֮��ĺ�����ϵʽ�������![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ��AC����O��ֱ����OB����O�İ뾶��PA����O�ڵ�A��PB��AC���ӳ��߽��ڵ�M����COB=��APB��

��1����֤��PB����O�����ߣ�
��2����OB=3��PA=6ʱ����MB��MC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com