
【题目】如图,反比例函数![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2![]() ,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求反比例函数的解析式;
(2)求tan∠DAC的值及直线AC的解析式.

【答案】(1)反比例函数为y=![]() (x>0);(2)tan∠DAC=
(x>0);(2)tan∠DAC=![]() ;直线AC的解析式为y=
;直线AC的解析式为y=![]() x﹣1.
x﹣1.
【解析】
试题(1)根据反比例函数图象上点的坐标特征易得k=2![]() , 从而求得反比例函数解析式;
, 从而求得反比例函数解析式;
(2)作BH⊥AD于H,如图,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2![]() ),确定AH=2
),确定AH=2![]() ﹣1,BH=2
﹣1,BH=2![]() ﹣1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=
﹣1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=![]() ;由于AD⊥y轴,则OD=1,AD=2
;由于AD⊥y轴,则OD=1,AD=2![]() , 然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=
, 然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=![]() x﹣1.
x﹣1.
试题解析:(1)由反比例函数y=![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2![]() ,1),得:k=2
,1),得:k=2![]() ×1=2
×1=2![]() ,
,
∴反比例函数为y=![]() (x>0);
(x>0);
(2)作BH⊥AD于H,如图,
把B(1,a)代入反比例函数解析式y=![]() (x>0),得a=2
(x>0),得a=2![]() ,
,
∴B点坐标为(1,2![]() ),
),
∴AH=2![]() ﹣1,BH=2
﹣1,BH=2![]() ﹣1,
﹣1,
∴△ABH为等腰直角三角形,
∴∠BAH=45°,
∵∠BAC=75°,
∴∠DAC=∠BAC﹣∠BAH=30°,
∴tan∠DAC=tan30°=![]() ;
;
∵AD⊥y轴,
∴OD=1,AD=2![]() ,
,
∵tan∠DAC=![]() =
=![]() ,
,
∴CD=2,
∴OC=1,
∴C点坐标为(0,﹣1),
设直线AC的解析式为y=kx+b,
把A(2![]() ,1)、C(0,﹣1)代入
,1)、C(0,﹣1)代入
得![]() ,解得:
,解得: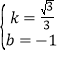 ,
,
∴直线AC的解析式为y=![]() x﹣1;
x﹣1;



 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
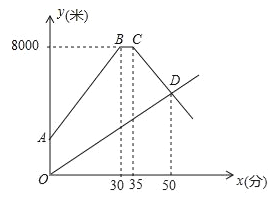
【题目】甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.
(1)求两人相遇时李伟离乙地的距离;
(2)请你判断:当张亮返回到甲地时,李伟是否到达乙地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB,BC,AC三边的长分别为![]() ,求这个三角形的面积,小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图所示,这样不需要求高,而借用网格就能计算出它的面积.请将△ABC的面积直接填写在横线上 .
,求这个三角形的面积,小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图所示,这样不需要求高,而借用网格就能计算出它的面积.请将△ABC的面积直接填写在横线上 .
思维拓展:我们把上述求△ABC面积的方法叫做构图法,若△ABC中,AB,BC,AC三边长分别为![]() ,2
,2![]() (a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,直接写出此三角形最长边上的高是 .
(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,直接写出此三角形最长边上的高是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
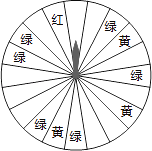
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
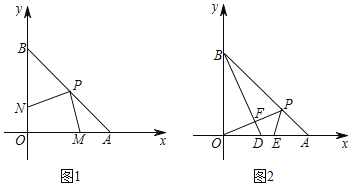
【题目】如图,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点.
(1)如图1,若P为AB的中点,点M、N分别是OA、OB边上的动点,且保持AM=ON,则在点M、N运动的过程中,探究线段PM、PN之间的位置关系与数量关系,并说明理由.
(2)如图2,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP,交OP、OA分别于F、D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上,下面有四个条件:
在同一直线上,下面有四个条件:
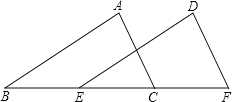
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
.请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
解:我写的真命题是:
已知:____________________________________________;
求证:___________.(注:不能只填序号)
证明如下:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com