Question

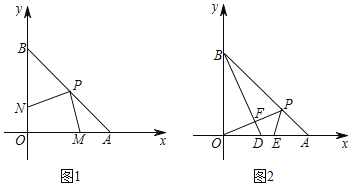
【题目】如图，在平面直角坐标系中，A、B坐标为（6，0）、（0，6），P为线段AB上的一点．

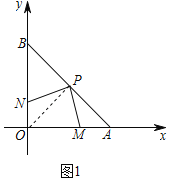
（1）如图1，若P为AB的中点，点M、N分别是OA、OB边上的动点，且保持AM＝ON，则在点M、N运动的过程中，探究线段PM、PN之间的位置关系与数量关系，并说明理由．

（2）如图2，若P为线段AB上异于A、B的任意一点，过B点作BD⊥OP，交OP、OA分别于F、D两点，E为OA上一点，且∠PEA＝∠BDO，试判断线段OD与AE的数量关系，并说明理由．

Answer 1

【答案】（1）PM＝PN，PM⊥PN，理由详见解析；（2）OD＝AE，理由详见解析．

【解析】

（1）连接OP．只要证明△PON≌△PAM即可解决问题；

（2）作AG⊥x轴交OP的延长线于G．由△DBO≌△GOA，推出OD＝AG，∠BDO＝∠G，再证明△PAE≌△PAG即可解决问题；

解：（1）结论：PM＝PN，PM⊥PN．理由如下：

如图1中，连接OP．

∵A、B坐标为（6，0）、（0，6），

∴OB＝OA＝6，∠AOB＝90°，

∵P为AB的中点，

∴OP＝AB＝PB＝PA，OP⊥AB，∠PON＝∠PAM＝45°，

∴∠OPA＝90°，

在△PON和△PAM中，，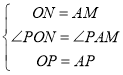

∴△PON≌△PAM（SAS），

∴PN＝PM，∠OPN＝∠APM，

∴∠NPM＝∠OPA＝90°，

∴PM⊥PN，PM＝PN．

（2）结论：OD＝AE．理由如下：

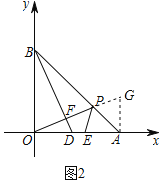
如图2中，作AG⊥x轴交OP的延长线于G．

∵BD⊥OP，

∴∠OAG＝∠BOD＝∠OFD＝90°，

∴∠ODF+∠AOG＝90°，∠ODF+∠OBD＝90°，

∴∠AOG＝∠DBO，

∵OB＝OA，

∴△DBO≌△GOA，

∴OD＝AG，∠BDO＝∠G，

∵∠BDO＝∠PEA，

∴∠G＝∠AEP，

在△PAE和△PAG中，，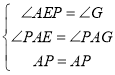

∴△PAE≌△PAG（AAS），

∴AE＝AG，

∴OD＝AE．