
【题目】如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求该反比例函数的解析式;
(2)求线段CD的长.

【答案】(1)y=![]() ;(2)4
;(2)4![]()
【解析】
(1) 根据给定线段的长度以及∠ABO的正切值可求出点C的坐标,结合点C的坐标利用待定系数法即可求出反比例函数的解析式;
(2)结合B,C点的坐标利用待定系数法即可求出一次函数的解析式,将一次函数解析式代入到反比例函数解析式中得关于x的一元二次方程,解方程即可求出D点的横坐标,将其代入反比例函数中即可求出D点的坐标,最后再由两点间的距离公式求出线段CD长度即可.
本题解析:
(1)设该反比例函数的解析式为y=![]() ,
,
∵tan∠ABO=![]() ,OB=4,OE=2,
,OB=4,OE=2,
∴CE=![]() (OB+OE)=3,
(OB+OE)=3,
∴点C的坐标为(﹣2,3).
∵点C在该反比例函数图象上,
∴3=![]() ,解得:m=﹣6.
,解得:m=﹣6.
∴该反比例函数的解析式为y=﹣![]() .
.
(2)∵点B(4,0),点C(﹣2,3)在一次函数y=kx+b的图象上,
∴有![]() ,解得:
,解得:![]() .
.
∴一次函数的解析式为y=﹣![]() x+2.
x+2.
令y=﹣![]() x+2=﹣
x+2=﹣![]() ,即x2﹣4x﹣12=0,
,即x2﹣4x﹣12=0,
解得:x=﹣2,或x=6.
∵当x=6时,y=﹣![]() =﹣1,
=﹣1,
即点D的坐标为(6,﹣1).
∵点C坐标为(﹣2,3),
∴CD=![]() =4
=4![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
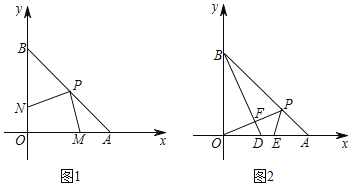
【题目】已知:如图1,△OAB是边长为2的等边三角形,OA在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.

(1)求在运动过程中形成的△OPQ面积S与运动时间t之间的函数关系,并写出自变量t的取值范围;
(2)在OA上(点O、A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
(3)如图2,现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点.
(1)如图1,若P为AB的中点,点M、N分别是OA、OB边上的动点,且保持AM=ON,则在点M、N运动的过程中,探究线段PM、PN之间的位置关系与数量关系,并说明理由.
(2)如图2,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP,交OP、OA分别于F、D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, ∠C = 90°,∠B= 30°,点D是线段AB的垂直平分线与BC的交点, 连接AD,则△ACD与△ADB的面积比为( )
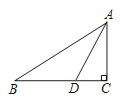
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x (时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:喝酒后几时血液中的酒精含量达到最大值?最大值为多少
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用![]() 元第一次购进一批服装,售完后又用
元第一次购进一批服装,售完后又用![]() 元购进同样的服装,件数是第一次件数的
元购进同样的服装,件数是第一次件数的![]() 倍,第二次比第一次每件贵了
倍,第二次比第一次每件贵了![]() 元.
元.
(1)商店两次共购进服装多少件?
(2)第一次以![]() 元/件很快销售完毕,第二次也以同样的价格销售,最后还剩
元/件很快销售完毕,第二次也以同样的价格销售,最后还剩![]() 件,然后又以
件,然后又以![]() 折的价格很快售完,请问该商店第二批服装的盈亏情况如何?
折的价格很快售完,请问该商店第二批服装的盈亏情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )

A.8.5B.15C.17D.34
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com