
分析 根据有理数运算的法则和整式加减的法则即可求出答案.
解答 解:(1)原式=-3$\frac{3}{7}$+$\frac{1}{8}$-6$\frac{4}{7}$+1$\frac{7}{8}$=-10+2=-8;
(2)原式=-64×$\frac{1}{8}$-$\frac{32}{33}$×$\frac{1}{8}$=-8$\frac{4}{33}$;
(3)原式=13×$\frac{2}{3}$+0.34×$\frac{2}{7}$+$\frac{1}{3}$×13+$\frac{5}{7}$×0.34=13×($\frac{2}{3}$+$\frac{1}{3}$)+0.34×($\frac{2}{7}$+$\frac{5}{7}$)=13+0.34=13.34;
(4)原式=4×$\frac{3}{2}$+32×$\frac{1}{4}$×$\frac{5}{4}$=6+10=16;
(5)原式=-2a2+a-4;
(6)原式=5a2b+3-6ab2-2a2b+8ab2=3a2b+2ab2+3.
点评 本题考查有理数的运算与整式加减运算,属于基础题型.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进出数量(t) | -4 | 5 | -2 | 3 | -3 |
| 进出次数 | 1 | 2 | 4 | 4 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠C=90°,且c=2a,则sinB的值为( )
如图,△ABC中,∠C=90°,且c=2a,则sinB的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
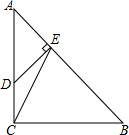 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE.求:
如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE.求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
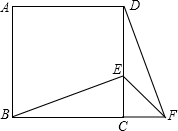 如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=70°,那么∠CEF的度数为( )
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=70°,那么∠CEF的度数为( )| A. | 20° | B. | 25° | C. | 40° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com