
【题目】如图①,在长方形ABCD中,E点在AD上,且∠ABE=40°,分别以BE、CE为折痕进行折叠并压平,如图②.若图②中∠BCE=n°,则∠AED的度数为_________°.(用含n的代数式表示)
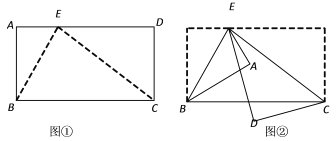
【答案】2n-80
【解析】由题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,即可得△ABE、△A′BE为直角三角形,然后可求得∠AED′的度数,又由∠BCE=n°,即可求得∠AED的度数.
解:根据题意得:∵∠A=∠A/=90°,△A′BE为直角三角形,
∴∠1=∠AEB=50°,
∵∠BCE=n°
∴∠AED/=180°-∠1-∠AEB=180°-50°-50°=80°,
∴∠DED/=∠AED+∠AED/=2n°,
∴∠AED=∠DED/–∠AED/=2=2n– 80°,
故答案为:2n– 80°.
“点睛”此题考查了折叠的性质、矩形的性质以及含30°角的直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意折叠中的对应关系.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如果一条抛物线的形状与y=﹣2x2+2的形状相同,且顶点坐标是(4,﹣2),则它的解析式是( )
A.y=2(x﹣4)2﹣2
B.y=﹣2(x﹣4)2﹣2
C.y=﹣2(x﹣4)2+2
D.y=﹣2(x+4)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合全面调查方式的是( )
A. 调查全国人民的环保意识 B. 调查中秋节期间市场月饼的质量
C. 调查某班40名同学的体重 D. 调查某类烟花爆炸燃放安全质量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有( )
①过两点有且只有一条直线.②连接两点的线段的长度叫做两点间的距离.③若AB=BC,则点B是AC的中点.④射线AC和射线CA是同一条射线.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阜阳某企业今年1月份产值为a万元,2月份比1月份减少了10%,预计3月份比2月份增加15%.则3月份的产值将达到( )
A. (a﹣10%)(a+15%)万元 B. (a﹣10%+15%)万元
C. a(1﹣10%)(1+15%)万元 D. a(1﹣10%+15%)万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=(m﹣n)x2+mx+n是二次函数的条件是( )
A.m、n是常数,且m≠0
B.m、n是常数,且m≠n
C.m、n是常数,且n≠0
D.m、n可以为任何常数
查看答案和解析>>
科目:初中数学 来源: 题型:
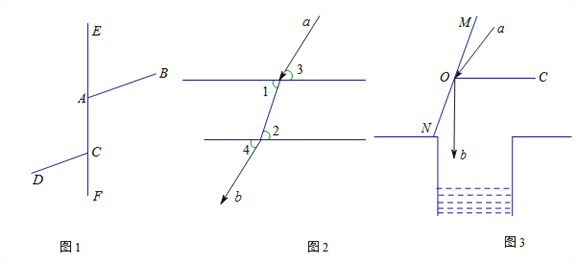
【题目】(1)光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图1,光线a从空气中射入水中,再从水中射入空气中,形成光线b,根据光学知识有∠1=∠2,∠3=∠4,请判断光线a与光线b是否平行,并说明理由;
(2)光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角等于反射光线与镜面的夹角,如图2有一口井,已知入射光线a与水平线OC的夹角为40°,问如何放置平面镜MN,可使反射光线b正好垂直照射到井底?(即求MN与水平线OC所夹的锐角);
(3)如图3,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,∠DCF=60°,射线AB、CD分别绕点A、点C以1度/秒和3度/秒的速度同时顺时针转动,设时间为t秒,在射线CD转动 一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com