
【题目】我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() 与
与![]() 的“广益值”就等于
的“广益值”就等于![]() 的值,可记为
的值,可记为![]()
(1)在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
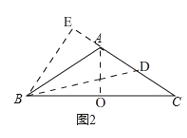
(2)如图2,在![]() 中,
中,![]() ,
,![]() ,求
,求![]() ,
,![]() 的值.
的值.
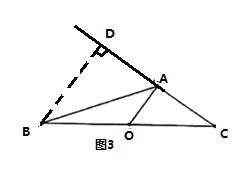
(3)如图3,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长.
的长.

【答案】(1)AC=9;(2)AB![]() AC=-72,BA
AC=-72,BA![]() BC=216;(3)BC=2OC=2
BC=216;(3)BC=2OC=2![]() ,AB=10.
,AB=10.
【解析】
(1)在Rt![]() 中,根据勾股定理和新定义可得AO2-OC2=81=AC2;
中,根据勾股定理和新定义可得AO2-OC2=81=AC2;
(2)①先利用含30°的直角三角形的性质求出AO=2,OB=![]() ,再用新定义即可得出结论;
,再用新定义即可得出结论;
②先构造直角三角形求出BE,AE,再用勾股定理求出BD,最后用新定义即可得出结论;
(3)作BD⊥CD,构造直角三角形BCD,根据三角形面积关系求出BD,根据新定义和勾股定理逆定理得出三角形AOD是直角三角形,根据中线性质得出OA的长度,根据勾股定理求出OC,从而得出BC,再根据勾股定理求出CD,再求出AD,再运用勾股定理求出AB.
(1)已知如图:AO为BC上的中线,
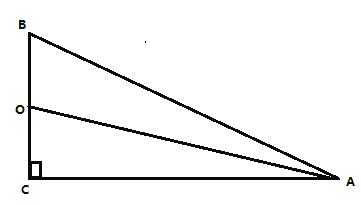
在Rt![]() 中,
中,
AO2-OC2=AC2
因为![]()
所以AO2-OC2=81
所以AC2=81
所以AC=9.
(2)①如图2,取BC的中点D,连接AO,∵AB=AC,∴AO⊥BC,
在△ABC中,AB=AC,∠BAC=120°,∴∠ABC=30°,
在Rt△AOB中,AB=12,∠ABC=30°,∴AO=6,OB=![]() =
=![]() ,
,
∴AB![]() AC=AO2﹣BO2=36﹣108=﹣72,
AC=AO2﹣BO2=36﹣108=﹣72,
②取AC的中点D,连接BD,∴AD=CD=![]() AC=6,过点B作BE⊥AC交CA的延长线于E,在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,∴∠ABE=30°,
AC=6,过点B作BE⊥AC交CA的延长线于E,在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,∴∠ABE=30°,
∵AB=12,∴AE=6,BE=![]() ,
,
∴DE=AD+AE=12,
在Rt△BED中,根据勾股定理得,BD=![]()
∴BA![]() BC=BD2﹣CD2=216;
BC=BD2﹣CD2=216;
(3)作BD⊥CD,
因为![]() ,
,![]() ,
,
所以BD=2![]() ,
,
因为![]() ,
,![]() 是
是![]() 边上的中线,
边上的中线,
所以AO2-OC2=-64,
所以OC2-AO2=64,
由因为AC2=82=64,
所以OC2-AO2= AC2
所以∠OAC=90°
所以OA=![]()
所以OC=![]()
所以BC=2OC=2![]() ,
,
在Rt△BCD中,
CD=![]()
所以AD=CD-AC=16-8=8
所以AB=![]()


科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一点,且
,D是AE上的一点,且![]() ,连接BD,CD.
,连接BD,CD.

![]() 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由;
![]() 如图2,若将
如图2,若将![]() 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
![]() 如图3,若将
如图3,若将![]() 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变.
![]() 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论;
![]() 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高人们对饮水品质的需求越来越高,岳阳市槐荫公司根据市场需求代理![]() ,
,![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多
型净水器进价多![]() 元,用
元,用![]() 万元购进
万元购进![]() 型净水器与用
型净水器与用![]() 万元购进
万元购进![]() 型净水器的数量相等
型净水器的数量相等
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元?
型净水器的进价各是多少元?
(2)槐荫公司计划购进![]() ,
,![]() 两种型号的共
两种型号的共![]() 台进行试销,,购买资金不超过
台进行试销,,购买资金不超过![]() 万元.试求最多可以购买
万元.试求最多可以购买![]() 型净水器多少台?
型净水器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了![]() ,
,![]() 两种型号的空气净化器,已知一台
两种型号的空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价多300元,用7500元购进
型空气净化器的进价多300元,用7500元购进![]() 型空气净化器和用6000元购进
型空气净化器和用6000元购进![]() 型空气净化器的台数相同.
型空气净化器的台数相同.
(1)求一台![]() 型空气净化器和一台
型空气净化器和一台![]() 型空气净化器的进价各为多少元?
型空气净化器的进价各为多少元?
(2)在销售过程中,![]() 型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划
型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划![]() 型净化器的进货量不少于20台且是
型净化器的进货量不少于20台且是![]() 型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
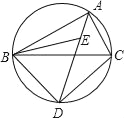
【题目】如图:△ABC是圆的内接三角形,∠BAC与∠ABC的角平分线AE、BE相交于点E,延长AE交圆于点D,连接BD、DC,且∠BCA=60°.
(1)求证:△BED为等边三角形;
(2)若∠ADC=30°,⊙O的半径为2![]() ,求BD长.
,求BD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F是AC上的动点,BD=DF
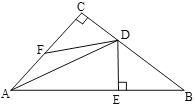
(1)求证:BE=FC;
(2)若∠B=30°,DC=2,此时![]() ,求△ACB的面积.
,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
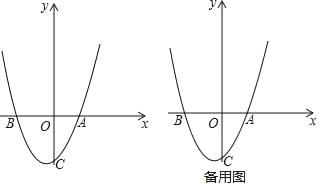
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(3,0),B(﹣5,0),C(0,﹣5)三点,O为坐标原点.
(1)求此抛物线的解析式;
(2)把抛物线y=ax2+bx+c(a≠0)向上平移![]() 个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
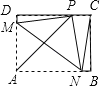
【题目】如图,在长方形纸片ABCD中,AB=12厘米,折叠纸片,使得点A落在CD边上的点P处,折痕为MN,点M、N分别在边AD、AB上,当点P恰好是CD边的中点时,点N与点B重合,若在折叠过程中NP=NC,则PD=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com