Question

【题目】如图1,在△ABC中,以AB为直径作⊙O分别交AC，BC于点D，E，且

（1）求证：AB=AC.

（2）若∠C=70°，求的度数.

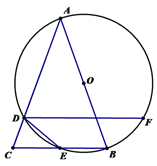
（3）如图2，点F在⊙O上， ，连结DF，DE.求证：∠ADF=∠CDE.

Answer 1

【答案】（1）证明见解析（2）100°（3）证明见解析

【解析】（1）连接AE，由圆周角定理得∠AEB=90°，再证⊿AEC≌⊿AEB即可得出AC=AB；（2）利用两弧的差即可求得弧AD的度数；(3) 利用等弧所对的圆周角相等，圆内接四边形的性质即可求得.

解：（1）连结AE，

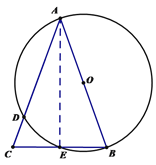
∵AB是直径，

∴∠AEB=900=∠AEC ，

∵弧DE=弧EB ，

∴∠CAE=∠EAB，

又∵AE=AE，

∴⊿AEC≌⊿AEB，

∴AC=AB.

（2）∵AB=AC，

∴∠B=∠C=700，

∴∠DAB=400，

∴ 弧DB=2∠DAB=800 ，

又∵AB是直径，

∴弧ADB =1800，

∴弧AD= 弧ADB -弧DB =1000 .

（3）∵弧BF=弧EB，AB为直径，

∴弧ADB=弧AFB=1800，

∴ 弧AF=弧AE，

∴∠ADF=∠B ，

又∵四边形ABED内接于圆O，

∴∠CDE=∠B，

∴∠ADF=∠CDE.