
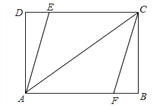
【题目】如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.

(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF×AF;
GF×AF;
(3)若![]() ,折痕AF=5
,折痕AF=5![]() cm,则矩形ABCD的周长为 .
cm,则矩形ABCD的周长为 .
【答案】(1)证明见解析;(2)证明见解析;(3)36cm.
【解析】试题分析:(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF。
(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可.
试题解析:
(1)证明:如图所示,
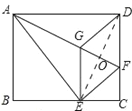
∵EG∥CD, ∴∠EGF=∠DFG.
∵由折叠的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG. ∴GD=DF.
∴GD=GE=DF=EF,∴四边形EFDG为菱形;
(2)证明:如图所示,连接DE,交AF于点O.
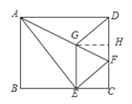
∵四边形EFDG为菱形, ∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA, ∴△DOF∽△ADF.
∴![]() ,即DF2=OFAF.
,即DF2=OFAF.
∵OF=![]() GF,DF=EG, ∴EG2=
GF,DF=EG, ∴EG2=![]() GFAF ;
GFAF ;
(3)矩形ABCD的周长为36 cm.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】关于反比例函数y=﹣ ![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.图像在第一、三象限
B.图像经过(2,1)
C.在每个象限中,y随x的增大而减小
D.当x>1时,﹣2<y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,∠A=36°.

(1)作∠ABC的平分线BD,交AC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)条件下,比较线段DA与BC的大小关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.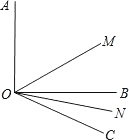
(1)已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,求∠MON的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( ) 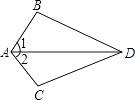
A.AB=AC
B.DB=DC
C.∠ADB=∠ADC
D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com