
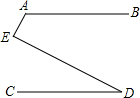
 如图所示,若AB∥CD,则∠A,∠D,∠E的度数之间的等量关系是∠A+∠E-∠D=180°.
如图所示,若AB∥CD,则∠A,∠D,∠E的度数之间的等量关系是∠A+∠E-∠D=180°. 科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺码 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量(双) | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com