
 如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和分析 (1)作PQ⊥AB交AB的延长线于H,根据三角形的外角的性质计算;
(2)设PQ=xm,根据正、余弦的定义表示出QH、BH,根据等腰直角三角形的性质列式计算即可.
解答 解:(1)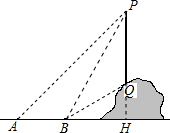 作PQ⊥AB交AB的延长线于H,
作PQ⊥AB交AB的延长线于H,
由题意得,∠QBH=30°,∠PBH=60°,
∴∠BQH=60°,∠PBQ=30°,
∴∠BPQ=∠BQH-∠PBQ=30°;
(2)设PQ=xm,
∵∠BPQ=∠PBQ,
∴BQ=PQ=xm,
∵∠QBH=30°,
∴QH=$\frac{1}{2}$BQ=$\frac{1}{2}$x,BH=$\frac{\sqrt{3}}{2}$x,
∵∠A=45°,
∴6+$\frac{\sqrt{3}}{2}$x=x$+\frac{1}{2}$x,
解得x=2$\sqrt{3}$+6≈9.
答:该电线杆PQ的高度约为9m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
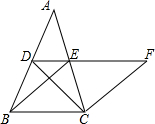 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
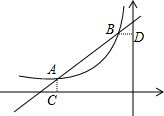 如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
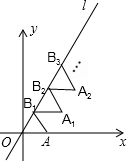 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2016的坐标是(1008,1008$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2016的坐标是(1008,1008$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
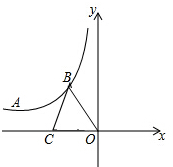 如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )
如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com