
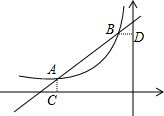
 如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.分析 (1)将点A、B的坐标代入一次函数解析式中,利用待定系数法即可求出一次函数的解析式;将点B的坐标代入反比例函数中,可得出关于m的一元一次方程,解方程即可得出结论;
(2)根据A、B点的坐标可以找出C、D点的坐标,由此可得出线段AC、BD的长度以及直线AC、BD的函数解析式,设点P的坐标为(m,$\frac{1}{2}$m+$\frac{5}{2}$),根据点到直线的距离以及三角形的面积公式可以得出关于m的一元一次方程,解方程即可得出m的值,代入到P点的坐标即可得出结论.
解答 解:(1)将A(-4,$\frac{1}{2}$),B(-1,2)代入一次函数解析式中,得$\left\{\begin{array}{l}{-4k+b=\frac{1}{2}}\\{-k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$.
故一次函数的解析式为y=$\frac{1}{2}$x+$\frac{5}{2}$.
将B(-1,2)代入反比例函数解析式中,得2=$\frac{m}{-1}$,
解得:m=-2.
(2)∵A(-4,$\frac{1}{2}$),B(-1,2),且AC⊥x轴于C,BD⊥y轴于D,
∴C(-4,0),D(0,2),
∴AC=$\frac{1}{2}$,BD=1,
直线AC的解析式为x=-4,直线BD的解析式为y=2,
设点P的坐标为(m,$\frac{1}{2}$m+$\frac{5}{2}$),
P点到直线AC的距离为|m-(-4)|,P点到直线BD的距离为|2-($\frac{1}{2}$m+$\frac{5}{2}$)|.
∵△PCA面积和△PDB面积相等,
∴$\frac{1}{2}$AC•|m-(-4)|=$\frac{1}{2}$BD•|2-($\frac{1}{2}$m+$\frac{5}{2}$)|,
解得:m=-$\frac{5}{2}$,
点P的坐标为(-$\frac{5}{2}$,$\frac{5}{4}$).
点评 本题考查了待定系数法求函数解析式、点到直线的距离以及三角形的面积公式,解题的关键是:(1)待定系数法求函数解析式;(2)找出关于m的一元一次方程.本题属于中档题,难度不大,(1)用到了待定系数法求函数解析式,这个是考试必考内容之一,再日常做题中应多加练习;(2)巧妙的利用点到直线的距离代替了高,减少了运算量.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某海域有A,B两个岛屿,B岛屿在A岛屿北偏西30°方向上,距A岛120海里,有一艘船从A岛出发,沿东北方向行驶一段距离后,到达位于B岛屿南偏东75°方向的C处,求出该船与B岛之间的距离CB的长(结果保留根号).
某海域有A,B两个岛屿,B岛屿在A岛屿北偏西30°方向上,距A岛120海里,有一艘船从A岛出发,沿东北方向行驶一段距离后,到达位于B岛屿南偏东75°方向的C处,求出该船与B岛之间的距离CB的长(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 最低气温(℃) | -1 | 0 | 2 | 1 |
| 天数 | 1 | 1 | 2 | 3 |
| A. | 2,3 | B. | 2,1 | C. | 1.5,1 | D. | 1,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com