
 某海域有A,B两个岛屿,B岛屿在A岛屿北偏西30°方向上,距A岛120海里,有一艘船从A岛出发,沿东北方向行驶一段距离后,到达位于B岛屿南偏东75°方向的C处,求出该船与B岛之间的距离CB的长(结果保留根号).
某海域有A,B两个岛屿,B岛屿在A岛屿北偏西30°方向上,距A岛120海里,有一艘船从A岛出发,沿东北方向行驶一段距离后,到达位于B岛屿南偏东75°方向的C处,求出该船与B岛之间的距离CB的长(结果保留根号). 分析 要求该船与B岛之间的距离CB的长,可以作辅助线AD⊥BC于点D,然后根据题目中的条件可以分别求得BD、CD的长,从而可以求得BC的长,本题得以解决.
解答 解:作AD⊥BC于点D,如下图所示,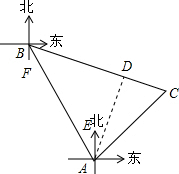
∵∠EAB=30°,AE∥BF,
∴∠FBA=30°,
又∵∠FBC=75°,
∴∠ABD=45°,
∵AB=120,
∴AD=BD=60$\sqrt{2}$,
∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,
∴∠C=60°,
∵AD=60$\sqrt{2}$,
∴CD=$\frac{AD}{tan60°}=\frac{60\sqrt{2}}{\sqrt{3}}=20\sqrt{6}$,
∴BC=BD+CD=($60\sqrt{2}+20\sqrt{6}$)海里.
点评 本题考查解直角三角形的应用-方向角问题,解题的关键是明确题意,作出合适的辅助线,找出所求问题需要的条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
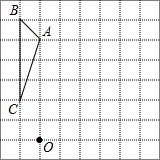 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,请完成下列任务:
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,请完成下列任务:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 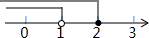 | C. | 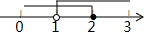 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
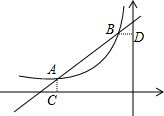 如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
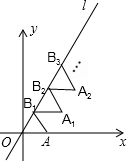 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2016的坐标是(1008,1008$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2016的坐标是(1008,1008$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com