
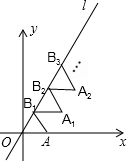
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2016的坐标是(1008,1008$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2016的坐标是(1008,1008$\sqrt{3}$). 分析 根据题意得出直线BB1的解析式为:y=$\sqrt{3}$x,进而得出B,B1,B2,B3坐标,进而得出坐标变化规律,进而得出答案.
解答 解:∵△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,
∴∠B1AO=60°,
∴B2016的横坐标是:1×2016×cos60°=2016×$\frac{1}{2}$=1008,
B2016的纵坐标是:1×2016×cin60°=2016×$\frac{\sqrt{3}}{2}$=1008$\sqrt{3}$,
故答案为:(1008,1008$\sqrt{3}$).
点评 此题主要考查了一次函数图象上点的坐标特征以及数字变化类,得出A点横纵坐标变化规律是解题关键.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
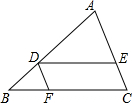 如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )
如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )| A. | $\frac{AD}{DB}$=$\frac{DE}{BF}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ | C. | $\frac{AE}{CE}$=$\frac{BF}{CF}$ | D. | $\frac{CE}{AC}$=$\frac{BF}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某海域有A,B两个岛屿,B岛屿在A岛屿北偏西30°方向上,距A岛120海里,有一艘船从A岛出发,沿东北方向行驶一段距离后,到达位于B岛屿南偏东75°方向的C处,求出该船与B岛之间的距离CB的长(结果保留根号).
某海域有A,B两个岛屿,B岛屿在A岛屿北偏西30°方向上,距A岛120海里,有一艘船从A岛出发,沿东北方向行驶一段距离后,到达位于B岛屿南偏东75°方向的C处,求出该船与B岛之间的距离CB的长(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 最低气温(℃) | -1 | 0 | 2 | 1 |
| 天数 | 1 | 1 | 2 | 3 |
| A. | 2,3 | B. | 2,1 | C. | 1.5,1 | D. | 1,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
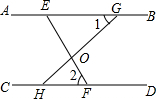 如图所示,AB∥CD,EF、HG相交于点O,∠1=40°,∠2=60°,则∠EOH的角度为( )
如图所示,AB∥CD,EF、HG相交于点O,∠1=40°,∠2=60°,则∠EOH的角度为( )| A. | 80° | B. | 100° | C. | 140° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和
如图,一电线杆PQ立在山坡上,从地面的点A看,测得杆顶端点A的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com