
分析 (1)根据题意可以直接写出y与x之间的函数关系式;
(2)根据题意可以直接写出w与x之间的函数关系式,由供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务可以确定x的取值范围;
(3)根据第(2)问中的函数解析式和x的取值范围,可以解答本题.
解答 解:(1)由题意可得,
y=200-(x-30)×5=-5x+350
即周销售量y(包)与售价x(元/包)之间的函数关系式是:y=-5x+350;
(2)由题意可得,
w=(x-20)×(-5x+350)=-5x2+450x-7000(30≤x≤40),
即商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式是:w=-5x2+450x-7000(30≤x≤40);
(3)∵w=-5x2+450x-7000的二次项系数-5<0,顶点的横坐标为:x=$-\frac{450}{2×(-5)}=45$,30≤x≤40
∴当x<45时,w随x的增大而增大,
∴x=40时,w取得最大值,w=-5×402+450×40-7000=3000,
即当售价x(元/包)定为40元时,商场每周销售这种防尘口罩所获得的利润w(元)最大,最大利润是3000元.
点评 本题考查二次函数的应用,解题的关键是明确题意,可以写出相应的函数解析式,并确定自变量的取值范围以及可以求出函数的最值.


科目:初中数学 来源: 题型:选择题
| A. | 若a:b=c:d,则ac=bd | |
| B. | 相似三角形的面积比等于相似比的平方 | |
| C. | 点C是线段AB的黄金分割点,且AC>BC,则$\frac{BC}{AB}=\frac{{3-\sqrt{5}}}{2}$ | |
| D. | 经过位似多边形对应顶点的直线一定交于同一点 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
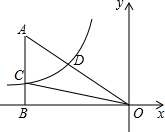 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△OAB斜边OA的中点D,且与直角边AB与相交于点C.若△COD的面积为6,则k的值为-8.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△OAB斜边OA的中点D,且与直角边AB与相交于点C.若△COD的面积为6,则k的值为-8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com