
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
【答案】D
【解析】分析:根据折叠的性质易知,重合部分为菱形,然后根据菱形的性质判断即可.
详解:∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,∴AB∥CD,AD∥BC,∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);
过点D分别作AB,BC边上的高为DE,DF.如图所示:
则DE=DF(两纸条相同,纸条宽度相同);
∵平行四边形ABCD的面积=AB×DE=BC×DF,∴AB=BC,∴平行四边形ABCD为菱形(一组邻边相等的平行四边形是菱形).
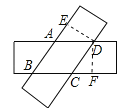
∵ABCD是菱形,∴∠ABC=∠ADC,∠BAD=∠BCD, AB=BC, AB=CD,AD=BC.故A、B、C正确.不能判断D是否正确.
故选D.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为![]() ,其中
,其中![]() .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.
数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为![]() ,AC边上的高
,AC边上的高![]() ,求
,求![]() 的值;
的值;
(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了扩大经营,决定购进6台机器用于生产某种活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示,经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为( )

A. (﹣![]() ,
,![]() ) B. (﹣
) B. (﹣![]() ,
,![]() ) C. (﹣
) C. (﹣![]() ,
,![]() ) D. (﹣
) D. (﹣![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
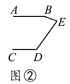
【题目】有一天李小虎同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从图②③④中,选一个说明它成立的理由.
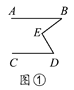
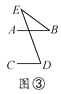
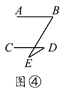
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且 ![]() =
= ![]() ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com