
【题目】有一天李小虎同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从图②③④中,选一个说明它成立的理由.
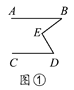
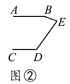
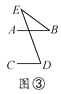
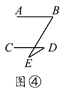
【答案】(1)(1)图①:∠BED=∠B+∠D;图②:∠B+∠BED+∠D=360°;图③:∠BED=∠D-∠B;图④:∠BED=∠B-∠D;(2)证明见解析.
【解析】
(1)过每个图形的拐点作平行线,利用平行线的性质即可解答;(2)选择③,过点E作EF∥AB,根据两直线平行,内错角相等可得∠D=∠DEF,∠B=∠BEF,再根据∠BED=∠DEF-∠BEF整理即可得证.
(1)图①:∠BED=∠B+∠D;
图②:∠B+∠BED+∠D=360°;
图③:∠BED=∠D-∠B;
图④:∠BED=∠B-∠D.
(2)以图③为例:如图,过点E作EF∥AB,
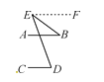
∵AB∥CD,
∴EF∥CD,
∴∠D=∠DEF,∠B=∠BEF.
∵∠BED=∠DEF-∠BEF,
∴∠BED=∠D-∠B.


科目:初中数学 来源: 题型:
【题目】在我县中小学读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类,学校根据调查情况进行了统计,并绘制了不完整条形统计图和扇形统计图.
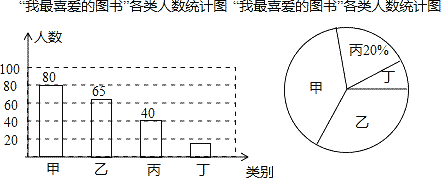
请你结合图中的信息,解答下列问题(其中(1)、(2)直接填答案即可);
(1)本次调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 人,最喜爱甲类图书的人数被调查人数的 %.
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校约有学生1800人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求回答问题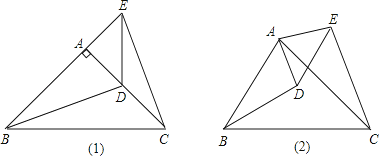
(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由.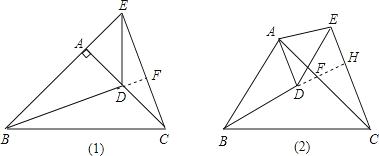
(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE在(1)中的位置关系仍然成立?不必说明理由.
甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;
乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;
丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有若干个数,第一个数记为a1,第二个数记为a2,第三个数记为a3,…,第n个数记为an,若a1=![]() ,从第二个数起,每个数都等于“1与它前面那个数差的倒数”.
,从第二个数起,每个数都等于“1与它前面那个数差的倒数”.
(1)计算:a2 ,a3 ,a4 ,a5的值;
(2)这排数有什么规律?由你发现的规律,计算a2014的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
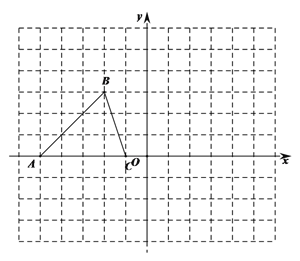
【题目】已知△ABC的三个顶点的坐标分别为A(﹣5,0)、B(﹣2,3)、C(﹣1,0)
(1)画出△ABC关于坐标原点O成中心对称的△A1B1C1;
(2)将△ABC绕坐标原点O顺时针旋转90°,画出对应的△A′B′C′,
(3)若以A′、B′、C′、D′为顶点的四边形为平行四边形,请直接写出在第四象限中的D′坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生孝敬父母的情况(选项:A为父母洗一次脚;B帮父母做一次家务;C给父母买一件礼物;D其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
根据以上信息解答下列问题:


(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=![]() ,OC=
,OC=![]() ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com